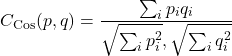Superposition – Management 4.0

Quantum Spiral Dynamics: ‚Es gibt nur eine Welt!‘ – Computer-experimentelle Metaphysik oder von Kohärenz und Kohäsion

Kurzfassung: Ich analysiere das Deutschland-Modell 2000–2025 des letzten Blog-Beitrages. Die Analyse mit Quantum Spiral Dynamics (QSD) zeigt eine deutliche Diskrepanz zwischen thematischer Kohäsion und narrativer Kohärenz. Während die klassischen Kohäsionsmaße relativ hoch bleiben und auf gemeinsame Themen verweisen, liegt die Quanten-Kohäsion fast konstant nahe null. Dies deutet auf fehlende phasenmäßige Resonanz und damit mangelnde gemeinsame Narrative der Themen hin. Die Kohärenz-Auswertung über alle Agenten zeigt, dass Ereignisse wie Agenda 2010, Eurokrise, Fluchtmigration oder Energiekrise kurzfristige negative Ausschläge in der Kohärenz verursachen. Insgesamt entsteht das Bild einer Gesellschaft, die zwar thematisch verbunden ist, jedoch keine gemeinsamen Narrative und keine dauerhafte kollektive Synchronisation erreicht: Ohne narrative Kohärenz ist die Gesellschaft instabil und anfällig für Brüche.

Diesen Blog-Beitrag habe ich nur mit ChatGPT 5.0 erstellt. Wie schon im vorhergehenden Blog hatte ich auch dieses Mal keine Probleme in der Bearbeitung mit ChatGPT. – Lediglich bei der Erstellung von Latex für WordPress und bei der Bildgenerierung gibt es Unzulänglichkeiten.
Da ich immer noch Anleitungen zum guten Prompting und der damit verbundenen KI-Unkenntnis in den sozialen Medien finde, will ich an dieser Stelle etwas zu meiner Arbeit mittels KI-Systemen sagen. Meine Blog-Beiträge entstehen typischer Weise in Zeiträumen von 4-6 Wochen. In diesen 4-6 Wochen setze ich iterativ mehrere hundert Prompts an die KI ab: Grundlegende Ideen kommen hierbei meistens von mir. Eine grundlegende Idee für diesen Blog-Beitrag ist, herauszuarbeiten welche Bedeutung Quanten-Kohärenz und -Kohäsion für kollektive Phänomene haben. Ich starte hierbei mit den Grundlagen in den Naturwissenschaften und transferiere zusammen mit ChatGPT diese Erkenntnisse auf soziale und psychische Fragestellungen. ChatGPT liefert hierbei die mathematischen Modelle und die dazugehörigen Programme; sehr oft auch mögliche fachliche Interpretationen. Alle KI-Aussagen werden vielmals iterativ quergeprüft: Ich tue dies, indem ich die KI-Aussagen selbst überprüfe und mit anderen KI-Aussagen vergleiche. Außerdem gebe ich der KI oft etwas andere Fragestellungen, lasse sie einen neuen Kontext bearbeiten oder stelle weiterführende Frage.
ChatGPT 5.0 nimmt meine Aussagen oder Fragestellungen auf und wiederholt diese mit wissenschaftlicher Präzision. In keiner der hunderten Kommunikationen ergaben sich falsche KI-Interpretationen oder -Halluzinationen. – Wenngleich bei der mathematischen Umsetzung auch Fehler geschehen.

Die Art, wie ich die KI verwende, setzt voraus, dass bei mir eine gute fachliche Basis vorhanden ist und ich gewillt bin, diese durch aktives iteratives Arbeiten und Lernen zu erweitern. – Ich kommuniziere hierbei mit der KI wie ich auch mit einem menschlichen Fachkollegen kommunizieren würde.
In der Vergangenheit habe ich DeepSeek, Mistral und Claude währende des Blog-Erstellungsprozesses zur Qualitätssicherung verwendet. – Inzwischen tue ich dies nur noch am Ende, wenn der Blog-Beitrag fast fertig ist.

Dieser Beitrag ist der dritte Beitrag der Blog-Reihe ‚Quantum Spiral Dynamics: ‚Es gibt nur eine Welt!‘ …‘.

In der Online-Zeitschrift Quanta Magazine erschien vor kurzem der Artikel „ ‚Metaphysical Experiments‘ Probe our Hidden Assumptions about Reality“ [1]. – Als philosophische Disziplin versucht die Metaphysik die Basis unseres Seins zu ergründen [2]: Sie stellt sich zum Beispiel Fragen wie ‚Was ist Realität?‘ ‚Ist diese Realität von uns als Beobachtern abhängig?‘ ‚Was sind Raum und Zeit?‘, ‚Sind Quanten real?‘ usw.. Die Experimentelle Metaphysik verbindet Physik und Philosophie, und versucht der Beantwortung dieser oder ähnlicher Fragen mittels Experimenten näher zu kommen. Meine Blog-Beiträge lassen sich sehr oft in diesem Bereich zwischen Wissenschaft und Philosophie verorten: Ich führe zwar keine Experimente durch, sondern benutze den Computer, um spekulative Gedanken mittels (Quanten-) Computer-Berechnungen oder -Simulationen auf ‚Sinnhaftigkeit‘ zu überprüfen. – Damit sind meine Ergebnis bei weitem nicht so stringent wie diejenigen, die mit Experimenten gewonnen werden. – Ich verwende Modelle und Theorien, die sich in der Physik bewährt haben, verändere diese für einen sozialen oder psychischen Kontext und überprüfe, ob daraus resultierende Aussagen ‚Sinn ergeben‘. ‚Sinn ergeben‘ heißt, dass die Ergebnisse durchaus mit der Brille ‚Sozial‘ oder ‚Psyche‘ interpretiert werden können und sogar einen Blick in die Zukunft gesellschaftlicher Entwicklungen erlauben. – Bisher hat sich diese Form von ‚Sinn ergeben‘ gezeigt, indem sich die metaphysische Tür zu ‚Es gibt nur eine Welt!‘ mit meinen Blog-Beiträgen ein wenig geöffnet hat.

Für diesen Blog-Beitrag formuliere ich zwei ‚metaphysische‘ Fragestellungen:

Lassen sich gesellschaftliche Phänomene wie Kultur oder Team Collective Mind mittels Potentialen oder Feldern beschreiben, wie man sie aus der Physik kennt?
Kann man soziale Resonanz zwischen Menschen mittels der Wellenmechanik der Quantenmechanik beschreiben?

Zur ersten Frage: Drei der vier Fundamentalkräfte (Elektrodynamik, starke Wechselwirkung und schwache Wechselwirkung) werden heute mit sogenannten Eichpotentialen beschrieben. Diese Eichpotentiale erzeugen sogenannte unitäre Dynamiken bzw. Transformationen. Ich verzichte hier auf die genaue mathematische Definition der unitären Dynamik. Wichtig ist hier, dass diese Eichpotentiale Information in einem modellierten System erhalten. Lediglich zwischen Teilsystemen eines System kann Information verschoben werden. Derzeit ist die vierte Kraft, die Gravitation, die einzige Wechselwirkung, die Information zerstört, denn sie wird derzeit über die Allgemeine Relativitätstheorie beschrieben, die keine Eichtheorie ist.- In dem Glauben, dass alle Fundamentalkräfte auf Eichpotentialen beruhen, wird seit Jahrzehnten versucht, die Allgemeine Relativitätstheorie in eine Eichtheorie einzubetten. – Bisher ohne Erfolg.
Es gibt auch einige Wissenschaftler – darunter der Nobelpreisträger Roger Penrose – die überzeugt sind, dass sich Gravitation nicht durch eine Eichtheorie beschreiben lässt und dass gerade dies notwendig ist, damit unsere makroskopische Realität aus der Quantenwelt hervorgehen kann.– Die Gravitation sorge hiernach dafür, dass der typische Wellencharakter der Quantenwelt ‚kollabiert‘ und die makroskopische Welt entsteht. – Zum ‚Kollabieren der Wellenfunktion‘ verweise ich auf den nachfolgenden Text.

Ich habe das SU(3) Eichpotential der starken Wechselwirkung für die Beschreibung gesellschaftlicher Phänomene gewählt, weil die Nicht-Kommutativität unserer Entscheidungen damit abgebildet werden kann (man siehe hierzu die vorherigen Blog-Beiträge). Außerdem lassen sich die Bewusstseinsebenen des Spiral Dynamics Modells problemlos auf die Freiheitsgrade des SU(3) Potentials abbilden. Die kulturelle Information bleibt erhalten und wird lediglich von einem Teilsystem in ein anderes Teilsystem transformiert.
Das SU(3) Eichpotential hat ursprünglich vier Komponenten, eine Zeitkomponente und drei Ortskomponenten. – Mit Einführung der Relativitätstheorie vor mehr als 100 Jahren haben fast alle physikalischen Größen diese Vierer-Struktur bekommen. Jede der vier Komponenten wird durch die 8 Generatoren und jeweils 8 Parameterfunktionen modelliert. Jede Parameterfunktion kann zusätzlich von Ort und Zeit abhängen. – Also eine ziemlich komplexe Struktur… Man siehe hierzu den Anhang des ersten Blog-Beitrages dieser Reihe.

Das in den letzten Blog-Beiträgen verwendete kulturelle Eichpotential ist (derzeit) ein Modell, das nur eine Ortskomponente enthält. Diese Ortskomponente enthält die Zeit als Parameter, aber nicht den Ort, ist also ohne Ortsauflösung: D.h. ohne Länder, Regionen, Organisationen oder Teams; aber mit Zeitauflösung. – Das heißt, das QSD-Kulturpotential hängt bisher nur von der Zeit aber nicht vom Ort ab. Im letzten Blog-Beitrag habe ich also Deutschland als homogenes Land für den Zeitraum 2000-2025 beschrieben. Die Teilsysteme des Systems Deutschland sind ‚nur‘ die drei Agenten mit ihren Werte-Ebenen im Spiral Dynamics Modell: Blau, Orange und Grün.

Mit der Zeit-Komponente hat man die Möglichkeit unterschiedliche Zeitskalen bzw. Frequenzen für die drei verwendeten Spiral Dynamics Ebenen zu modellieren: Die Grüne Ebene ‚tickt‘ dann zum Beispiel anders als die blaue Ebene und die Kopplung der Uhren dieser Ebenen kann auch abgebildet werden. Dies könnte ein Thema für einen der nächsten Blog-Beiträge sein.

Mit meiner Wahl der Potential-Komponenten habe ich die einfachste Eichung für das Kulturpotential vorgenommen. – Die vorherigen beiden Blog-Beiträge haben meines Erachtens gezeigt, dass diese Eichung für die Modellierung gesellschaftlicher Phänomene schon aussagekräftige Ergebnisse liefert.

Zur zweiten Frage: Die Frage nach der Abbildbarkeit von zwischenmenschlicher Resonanz mittels Wellenmechanik führt mich unmittelbar zu den Begriffen Kohärenz und Kohäsion. Ich definiere nämlich Resonanz als das Auftreten von Kohärenz und ggf. Kohäsion in der Wellenmechanik:

Kohärenz misst Synchronisation: Quanten oder Agenten schwingen im Takt, gleichzeitig oder versetzt. Über Phasenbeziehungen werden Quanten oder Agenten (bzw. deren Werte) in Superposition gebracht. – Es entstehen hieraus neue Zustände, die als Ganzes wirken und Interferenzen ausbilden.
Kohäsion misst Bindung: Quanten oder Agenten werden durch Kräfte oder Rahmenbedingungen (u.a. Strukturen und Institutionen) zusammengehalten. Dies erzeugt Stabilität und Ordnung.

Kohärenz und Kohäsion sind zwei unabhängige Größen, so kann zum Beispiel Synchronisation zunehmen, während Bindung abnimmt.

Ich verdeutliche Kohärenz und Kohäsion an einem Beispiel aus der Filmwelt: Es gibt sehr viele Filme, in denen zwei sehr ungleiche Personen durch einen meist unglücklichen Umstand (Rahmenbedingung) auf einander angewiesen sind, um eine Aufgabe zu meistern. Durch diese ungewollte Kohäsion beginnen sie nach einiger Zeit immer mehr ihre Handlungen aufeinander abzustimmen. Diese Form der Kohärenz führt dazu, dass sie besonders erfolgreich sind. Sie agieren als Team, also als Ganzes.

Oder ein anderes Beispiel: Bei einem Liebespaar wirkt die gegenseitige Attraktivität als Kohäsion und die Kohärenz stellt sich als gemeinsames Denken und Handeln (manchmal) danach ein.

Deshalb haben wir ehemals definiert, dass ein Team oder eine Organisation ein Collective Mind zeigt, wenn sowohl Kohäsion als auch Kohärenz vorliegen. – Für eine mathematische Definition der beiden Begriffe im Kontext der QSD verweise ich auf den Anhang.

Abbildung 1 gibt Beispiele aus der Physik und der Gesellschaft und verdeutlicht diese mittels der Einordnung in eine 2*2 Matrix für Kohäsion und Kohärenz.

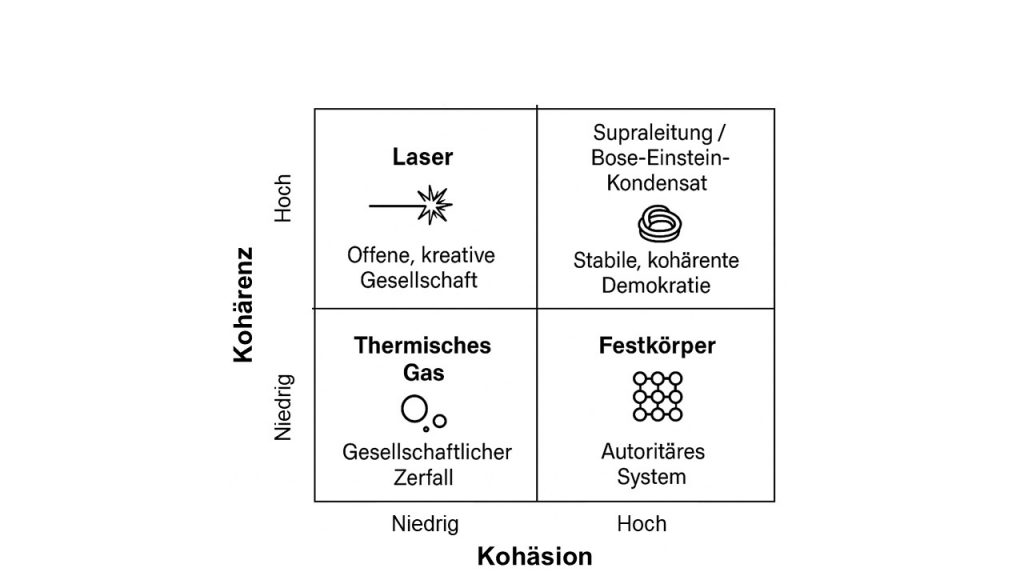
Abbildung 1: Erstellt unter Mitwirkung von ChatGPT. Eine 2*2 Matrix für Kohäsion und Kohärenz zeigt Beispiele aus Physik und Gesellschaft. Die Physik Beispiele zu Laser und Supraleitung verwende ich oft in Management 4.0 Trainings, um die ‚unglaubliche‘ Leistung von kohäsiven und kohärenten Systemen zu verdeutlichen: Mit einem Laser können wir sehr große Energie auf kleinstem Raum bündeln, also zum Beispiel Stahlplatten durchschneiden. Die Supraleitung dient dazu, elektrische Ströme widerstandlos zu erzeugen. – In beiden Fällen muss man eine gewisse Energie in das System eingeben, um die gewünschten Effekte zu erzielen. Ich erläutere kurz was bei der Supraleitung geschieht: Spezielle Materialien werden auf sehr tiefe Temperaturen abgekühlt.- Um dies zu erreichen, benötigt man eine gewisse Energie. Die Gitteratome der Materialien zeigen bei sehr tiefen Temperaturen nur noch sogenannte Ruheschwingungen, man spricht von virtuellen Quanten, den Phononen. Zwei Elektronen treten über die Phononen in Wechselwirkung, sie bilden also eine Kohäsion aus. Liegt diese Kohäsion vor, ist die Voraussetzung geschaffen, dass sich ein (bosonisches) Elektronenpaar, das sogenannte Cooper-Paar, in Kohärenz ausbildet. In dem alle Cooper-Paare in einen gemeinsamen kohärenten Zustand übergehen, senkt sich die Energie noch weiter ab. – Es entsteht Supraleitung: Das Ganze ist mehr als die Summe seiner Teile. – Dies ist wahrscheinlich das beste physikalische Beispiel für Kohäsion und Kohärenz.

Wie man aus Abbildung 1 entnehmen kann, tritt Kohäsion sowohl in makroskopischen Systemen (Festkörper) als auch in Quantensystemen (Supraleiter) auf. Kohärenz, wie wir sie gleich skizzieren, ist ein typischer Quanteneffekt: Die Wellen der Quanten wechselwirken miteinander. Ich benutze diesen Effekt der Wellenmechanik, um interfrierende Wechselwirkung der Entscheidungsfindung im Menschen (Quantum Cognition) und in der Kommunikation zwischen Menschen zu beschreiben. – Es ist (bisher?) lediglich ein Modell, das psychische und soziale Effekte hilft mathematisch zu erfassen. – Unter dieser Einschränkung stehen die Ergebnisse dieser Blog-Reihe!

Ich habe überprüft, inwieweit die Zuordnung der Basiszustände zu den Generatoren sowie die Zuordnung der Basiszustände zu den Werte-Farben und die Zuordnung der Parameterfunktionen zu den Generatoren einen Einfluss auf die bisherigen und nachfolgenden Ergebnisse haben:

Im QSD-Modell wird die gesellschaftliche Dynamik durch eine Zuordnung von Spiral Dynamics Farben zu quantenmechanischen Basiszuständen beschrieben. Diese Basiszustände sind nicht frei wählbar, sondern stehen in einem festen Zusammenhang mit den SU(3)-Generatoren, die das soziale Eichpotential aufspannen. Mathematisch gilt: Jede unitäre Permutation der Basis wäre erlaubt, weil sich die Generatoren konsistent transformieren lassen. Inhaltlich jedoch zeigt ein Permutationstest, dass nicht alle Zuordnungen von Farben zu Basiszuständen gleichwertig sind.
Die Referenzzuordnung der Zustände zu Blau, Orange und Grün repoduziert die Daten des Deutschland-Modells 2000 bis 2025 über die Zeit am konsistentesten. Andere Permutationen sind zwar formal korrekt, führen aber u.a. zu abweichenden Phasen- und Kohärenzverläufen, die mit den empirischen Entwicklungen in Deutschland von 2000 bis 2025 weniger gut in Einklang stehen.
Die Wahl der Zuordnungen entsteht also nicht durch eine willkürliche Setzung, sondern spiegelt eine Konsistenz zwischen mathematischer Struktur (Basis und Generatoren) und sozialer Interpretation (Farbwerte und Parameterfunktionen) wider. Sie liefert damit zugleich eine Validierung des Modells.

Die nachfolgende Formel zeigt die allgemeinste Form einer Superposition für den Werte-Zustand eines Menschen in dem vereinfachten QSD-Modell, bestehend aus den Ebenen Blau (b), Orange (o) und Grün (g). Die Argumente in den e-Funktionen sind die Phasen der Wellenfunktionen: Vergegenwärtigt man sich, dass die e-Funktion mit komplexem Argument auch mittels cos- und sin-Funktion dargestellt werden kann, so sieht man, dass über diese Wellen-Wechselwirkungen (u.a. Superpositionen und Interferenzen) entstehen:

$\begin{equation*} |\Psi_{\text{QSD}}(t,r)\rangle = c_b\,e^{\,i\,\theta_b(t,r)}\,|b\rangle \;+\; c_o\,e^{\,i\,\theta_o(t,r)}\,|o\rangle \;+\; c_g\,e^{\,i\,\theta_g(t,r)}\,|g\rangle \end{equation*}$

Ѳ bezeichnet die Phasen, ist reel und hängt von der Zeit t und dem Ortsvektor r ab.

Jeder der Agenten mit einem der Anfangs-Werte Blau, Orange und Grün wird auf seinem Weg im Kulturpotential durch solch eine Gleichung beschrieben: Am Anfang der Simulation der vorherigen Blog-Beiträge haben die Agenten nur eine Ausrichtung in den Werten, sie sind Blau oder Orange oder Grün. Während sie sich durch das Kulturpotential bewegen, geht ihre Werte-Zusammensetzung jeweils in eine Werte-Superposition über.

Abbildung 2 zeigt die Phasenentwicklung der Agenten und die Agenten-eigene Kohärenz gemäß dem Deutschland-Modell 2000-2025 des vorherigen Blog-Beitrags.

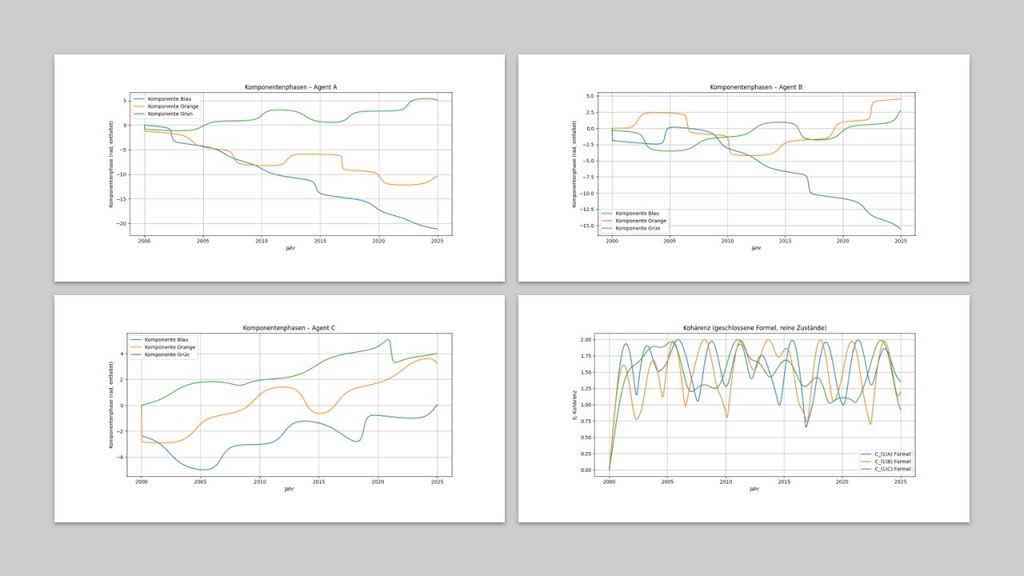
Abbildung 2: Die Abbildung zeigt jeweils die Entwicklung der drei Phasen der drei Agenten A (Blau), B (Orange) und C (Grün) sowie die daraus abgeleitete Agenten-eigene Kohärenz im Zeitraum 2000 bis 2025. In den Phasenverläufen wird deutlich, dass sich die Agenten unterschiedlich stark von ihrer ursprünglichen Basis entfernen: Während bei Agent A die Komponenten zunehmend auseinanderlaufen und damit eine wachsende interne Spannung andeuten, zeigen die Phasen von Agent B eine Polarisierung zwischen Blau sowie Orange und Grün, die auf eine innere Spaltung des Werteprofils hindeutet. Agent C hingegen bleibt phasenmäßig elastischer und oszilliert ohne eine klare Drift, was auf eine höhere Anpassungsfähigkeit im Werte- und Bedürfnisraum schließen lässt. Im Kontext der QSD bedeutet dies, dass A und B auf stabile, aber polarisierte Erzählrichtungen zusteuern, während C eher eine vermittelnde Rolle einnimmt bzw. einnehmen kann.

Abbildung 3 zeigt Kohärenz und Kohäsion für das 3 Agenten System:

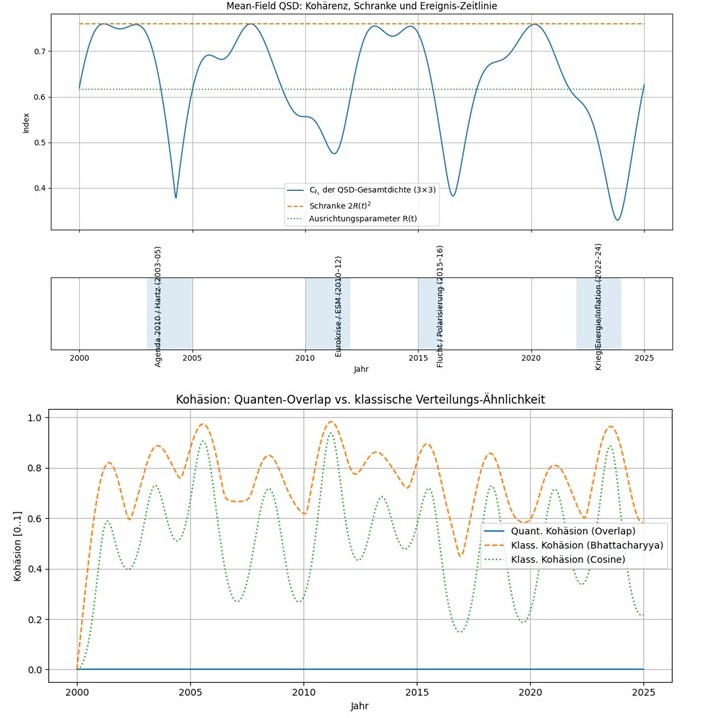
Abbildung 3: Diese Abbildung zeigt die Entwicklung von Kohärenz (oben) und Kohäsion (unten) im Deutschlandmodell 2000–2025. – Wir betrachten die drei Agenten Blau, Orange und Grün als Werte-Populationen mit einer 50%:30%:20% Verteilung.
Kohäsion bedeutet, dass Menschen ähnliche Themen bewegen, auch wenn sie unterschiedliche Narrative dazu haben. Kohärenz heißt, dass diese Themen in einer gemeinsamen Welle getragen werden, also in Resonanz geraten – sie teilen die gleichen Narrative.

Das Modell zeigt, dass die Gesamt-Kohärenz zwar zeitweise hohe Werte erreicht, jedoch bei zentralen Krisen – etwa Agenda 2010 (2004), Eurokrise (2012), Fluchtmigration (2016) und Energiekrise/Ukrainekrieg (2023) – tiefe Einbrüche erfährt. Die quantenmechanisch berechnete Kohäsion bleibt bei nahezu null, während die klassische Kohäsion (Bhattacharyya und Cosine) beständig belegt, dass es thematische Überschneidungen gibt.

Im Zusammenspiel ergibt sich: Wirtschaft, soziale Fragen oder Klima betreffen zwar alle, verlaufen aber in getrennten Erzählungen ohne dauerhaftes kollektives Narrativ. Ereignisse erzeugen kurzfristige Resonanz oder Brüche, doch keine stabile gemeinsame Phase. Deutschland zeigt somit thematische Kohäsion, aber keine narrative Kohärenz – also eine fragile Stabilität, die anfällig für Fragmentierung ist.

Ich beantworte also die zweite Frage, ob man soziale Resonanz zwischen Menschen mittels der Wellenmechanik der Quantenmechanik beschreiben kann, mit ja: Alle bisherigen QSD-Interpretationen sind konsistent und stimmen gut mit der Kultur-Realität in Deutschland überein.

Anhang

QSD Formeln und Erläuterung

Die nachfolgende Gleichung zeigt die QSD-Wellenfunktion in der allgemeinsten Form als Superpostion der Werte Blau, Orange und Grün. Jeder Agent wird durch solch eine Wellenfunktion beschrieben. Das Argument in der e-Funktion wird als Phase bezeichnet und ist für die Welleneigenschaften der Funktion verantwortlich: Eine imaginäre e-Funktion kann mittels cos- und sin-Funktion beschrieben werden, was den Wellencharakter sofort verständlich macht. Am Anfang der Simulation zeigen die Agenten jeweils ein ‚reines‘ Werteprofil, also nur jeweils Blau, Orange oder Grün:

$\begin{equation*} |\Psi_{\text{QSD}}(t,r)\rangle = c_b\,e^{\,i\,\theta_b(t,r)}\,|b\rangle \;+\; c_o\,e^{\,i\,\theta_o(t,r)}\,|o\rangle \;+\; c_g\,e^{\,i\,\theta_g(t,r)}\,|g\rangle \end{equation*}$

Falls ein Mehr-Quantensystem, oder im Falle der QSD, ein Mehr-Agenten System vorliegt, beschreibt man dieses sehr oft mittels eines Dichte-Operators bzw. einer Dichte-Matrix. Dass es sich bei dem Dichte-Operator um eine Matrix handelt, kann man sehr schnell sehen, wenn man die rechte Seite der nachfolgenden Gleichung als Vektorprodukt eines Vektors mit seinem transponierten Vektor interpretiert:

$\begin{equation*} \rho_{\text{QSD}}(t,r) \;=\; |\Psi_{\text{QSD}}(t,r)\rangle \langle \Psi_{\text{QSD}}(t,r)| \end{equation*}$

Man kann die Dichte-Matrix in einen Diagonalteil und einen Nicht-Diagonal-Teil zerlegen. Die Elemente des Nicht-Diagonal-Teils sind für die Kohärenz eines Quantensystems verantwortlich. Sind alle Nicht-Diagonal-Elemente null, geht das System in ein klassisches System über. – Es kollabiert. – Die nachfolgenden Gleichungen zeigen die Diagonal-Elemente und die Nicht-Diagonal-Elemente:

$\begin{equation*} \rho_{\text{QSD}}(t,r) \;=\; \rho_{\text{diag}}(t,r) \;+\; \rho_{\text{off}}(t,r) \end{equation*}$

$\begin{equation*} \rho_{\text{diag}}(t,r) \;=\; |c_b|^2\,|b\rangle\langle b| \;+\; |c_o|^2\,|o\rangle\langle o| \;+\; |c_g|^2\,|g\rangle\langle g| \end{equation*}$

$\begin{equation*} \rho_{\text{off}}(t,r) \;=\; \sum_{i\neq j \in {b,o,g}} \rho_{ij}(t,r)\,|i\rangle\langle j| \end{equation*}$

$\begin{equation*} \rho_{bo}(t,r) \;=\; c_b\,c_o\*e^{\,i\big(\theta_b(t,r)-\theta_o(t,r)\big)} \end{equation*}$

$\begin{equation*} \rho_{bg}(t,r) \;=\; c_b\,c_g\*e^{\,i\big(\theta_b(t,r)-\theta_g(t,r)\big)} \end{equation*}$

$\begin{equation*} \rho_{ob}(t,r) \;=\; c_o\,c_b\*e^{\,i\big(\theta_o(t,r)-\theta_b(t,r)\big)} \end{equation*}$

$\begin{equation*} \rho_{gb}(t,r) \;=\; c_g\,c_b\*e^{\,i\big(\theta_g(t,r)-\theta_b(t,r)\big)} \end{equation*}$

$\begin{equation*} \rho_{go}(t,r) \;=\; c_g\,c_o\*e^{\,i\big(\theta_g(t,r)-\theta_o(t,r)\big)} \end{equation*}$

$\begin{equation*} \text{(Hermitizität:)}\qquad \rho_{ji}(t,r) \;=\; \rho_{ij}(t,r)^{*}\, \end{equation*}$

Agenten-eigene Kohärenz

Ich beschreibe die zeitabhängige Agenten-eigene Kohärenz über die sogenannte C $\ell_1$ -Kohärenz. Diese misst die Stärke der Superposition über die Nicht-Diagonal-Elemente der Dichtematrix $:$

$\begin{equation*}C_{\ell_1}(\rho) = \sum_{i \neq j} \big| \rho_{ij} \big|.\end{equation*}$

Mean-Field Ansatz für die kollektive Kohärenz

Im Rahmen des QSD-Modells habe ich einen Mean-Field-Ansatz für die kollektive Kohärenz einer Agenten-Mischung eingeführt. Mit der Agenten-Mischung lassen sich Werte-Populationsmischungen einer Gesellschaft analysieren. Für Deutschland habe ich angenommen, dass 50% der Bevölkerung ein dominantes blaues Mem haben, 30% ein dominates orangenes und 20% ein dominates grünes Mem.

Zunächst definieren wir den kollektiven Zeiger als gewichtete Summe der Agentenzustände $\psi_n \in \mathbb{C}^3$ :

$\begin{equation*}\mu(t) = \sum_{n} w_n \psi_n(t),\qquad \sum_{n} w_n = 1.\end{equation*}$

Die Norm dieses Zeigers liefert den Ausrichtungsparameter $R(t)$ :

$\begin{equation*}R(t) = |\mu(t)| \in [0,1].\end{equation*}$

$R(t) \approx 0$ : die Agentenzustände heben sich gegenseitig auf → keine kollektive Ausrichtung.
$R(t) \approx 1$ : perfekte Ausrichtung → maximale Kohärenz.

Auf Basis von $R(t)$ konstruieren wir die Mean-Field QSD-Dichte-Matrix:

$\begin{equation*}\rho_{\text{QSD}}(t) = \big(1-R(t)^2\big) \mathrm{diag} \big(p_{\text{avg}}(t)\big)+ R(t)^2 \frac{|\mu(t)\rangle\langle\mu(t)|}{\langle \mu(t)|\mu(t)\rangle},\end{equation*}$

wobei $p_{\text{avg}}(t)=\mathrm{diag}\!\big(\rho_{\text{mix}}(t)\big)$ die klassische Durchschnittsverteilung über die Agenten bezeichnet.

Die Kohärenz wird mit dem C $\ell_1$ -Maß über die Nicht-Diagonal-Elemente von $\rho_{\text{QSD}}(t)$ berechnet:

$\begin{equation*}C_{\ell_1}(t) = \sum_{i\neq j} \big|\rho_{\text{QSD},ij}(t)\big|.\end{equation*}$

Für die Mean-Field-Formel kann dies kompakt in Abhängigkeit von $\hat{\mu}(t)=\mu(t)/\|\mu(t)\|$ geschrieben werden:

$\begin{equation*}C_{\ell_1}(t) = R(t)^2 \left[ \left(\sum_{i=1}^3 |\hat{\mu}_i(t)| \right)^2 - 1 \right].\end{equation*}$

Damit ergibt sich eine natürliche Schranke für die Kohärenz:

$\begin{equation*}C_{\ell_1}(t) \leq 2 R(t)^2,\end{equation*}$

wobei das Maximum genau dann erreicht wird, wenn alle drei Komponenten von $\hat{\mu}(t)$ gleiche Beträge besitzen, also

$\begin{equation*}|\hat{\mu}_b| = |\hat{\mu}_o| = |\hat{\mu}_g| = \tfrac{1}{\sqrt{3}}.\end{equation*}$

Quanten-Kohäsion (Overlap)
Dieses Maß berechnet die Überlappung zweier Zustände im Hilbert-Raum. Es ist sensitiv für Phasenbeziehungen und nimmt Werte im Bereich [0,1] an, wobei 1 volle Überdeckung (identische Zustände) bedeutet.
Im QSD-Kontext zeigt ein hoher Wert, dass Menschen nicht nur ähnliche Themen haben, sondern diese auch in gemeinsamer Phase und Resonanz bewegen – also ein Narrativ-Kollektiv bilden.

$\begin{equation*} \text{Cohesion}(t) = \frac{1}{\binom{N}{2}} \sum_{i<j} \big|\langle \Psi_i(t) | \Psi_j(t) \rangle \big| \end{equation*}$

Bhattacharyya-Kohäsion
Dieses Maß berechnet die Ähnlichkeit zweier Wahrscheinlichkeitsverteilungen, indem es deren geometrisches Mittel bildet. Es liegt im Bereich [0,1] wobei 1 für identische Verteilungen steht. Hierbei sind p_i und q_i die klassischen Wahrscheinlichkeiten, dass die Agenten in den Basis-Zuständen i (z. B. Blau, Orange, Grün) gemessen werden.

Im QSD-Kontext bedeutet ein hoher Wert: Menschen bewegen ähnliche Themen mit vergleichbarer Stärke, auch wenn ihre Narrative unterschiedlich sein können.

$\begin{equation*} C_{\text{Bhat}}(p,q) = \sum_{i} \sqrt{p_i q_i,} \end{equation*}$

$\begin{equation*} \quad p_i = | \psi_i |^2, q_i = | \phi_i |^2 \end{equation*}$

Kosinus-Kohäsion
Dieses Maß betrachtet die Verteilungen als Vektoren und misst den Winkel zwischen ihnen. Werte nahe 1 bedeuten eine sehr ähnliche Richtung (also ähnliche Verteilungen), Werte nahe 0 zeigen starke Unterschiede. Auch hier sind p_i und q_i die klassischen Wahrscheinlichkeiten für den jeweiligen Basiszustand i.

Im QSD-Kontext beschreibt dieses Maß, ob verschiedene Gruppen ihre Themen in vergleichbarer Gewichtung anordnen – ob also die „Richtung der Aufmerksamkeit“ ähnlich ist, auch wenn die absolute Stärke variiert.

$\begin{equation*} C_{\text{Cos}}(p,q) = \frac{\sum_{i} p_i q_i}{\sqrt{\sum_{i} p_i^2},\sqrt{\sum_{i} q_i^2}} \end{equation*}$

AI & QC & M 4.0: Quantum Cognition für das Team-Management oder von der Macht der Mathematik

(Die in diesem Blog-Beitrag enthaltene recht komplexe Mathematik der Quantenmechanik sowie die dazugehörigen Programme wurden mit der AI-Assistenz von ChatGPT4o1-preview erhalten. ChatGPT4o wurde für die Überprüfung des Blog-Beitrages verwendet. Der enthaltene Podcast wurde von der Google AI noteBookLM erstellt.)

Der nachfolgender Podcast fasst den Blog-Beitrag in englischer Sprache zusammen und wurde von der Google AI notebookLM erzeugt:

Abbildung 0: Ein Bild, erzeugt von ChatGPT/DALL.E, das den Blog-Beitrag visuell unterstützt und im Stil von van Gogh gestaltet ist. Es zeigt Teammitglieder in einer dynamischen Interaktion, die die Konzepte der Quantum Cognition durch wellenartige Verbindungen symbolisiert.

Dieser Blog-Beitrag richtet sich an Leser mit einem Hintergrund in Management sowie an jene, die Interesse an quantenmechanischen Konzepten im Bereich der Kognition und Teamdynamik haben: Keine Angst vor Mathematik ist hilfreich!

Bei den Recherchen zu dem vorherigen Quantum Computing Blog-Beitrag bin ich auf den Begriff ‚Quantum Cognition‘ gestoßen [1]. Sofort wenn man den Wikipedia Artikel oder die wissenschaftlichen Artikel [2],[3] liest, wird man darauf hingewiesen, dass Quantum Cognition nichts mit Quantum Mind [4] oder der Idee, dass Bewusstsein durch Quanteneffekte hervorgerufen wird, zu tun hat. – Wenngleich das letzte Wort hierzu sicherlich noch nicht gesprochen ist.

Bei dem Thema Quantum Cogition geht es um die verblüffende Feststellung, dass kognitive Verzerrungen wie u.a. Tversky und Kahneman sie beschrieben haben [5], schlecht oder überhaupt nicht durch die klassische Wahrscheinlichkeitstheorie (Classical Probability Theory) beschrieben werden, aber sehr wohl durch die Quanten Wahrscheinlichkeitstheorie (Quantum Probability Theorie), wie sie im mathematischen Formalismus der Quantenmechanik enthalten ist. Das ist schon irgendwie faszinierend…und zeigt meines Erachtens die ungeheure Macht der Mathematik: Denn plötzlich wird ein mathematischer Formalismus, der in einem Gebiet entwickelt wurde, auf einem völlig anderen Gebiet angewendet.

Ich beschäftige mich in diesem Blog-Beitrag zuerst mit den Grundlagen von Quantum Cognition. Anschließend wende ich diese Grundlagen auf die Teamkommunikation an. Bei der Konzeption des Collective Mind vor ca. zwei Jahrzehnten kam die Idee auf, den Collective Mind als sogenannten verschränkten Zustand der mentalen Modelle der Teammitglieder zu verstehen. Ich werde zeigen, dass mit dem Formalismus der Quantum Cognition genau dies möglich ist. Damit ergänze ich die in den vorhergehenden Blog-Beiträgen beschriebenen klassischen Modelle des Collective Mind. – In zukünftigen Blog-Beitragen besteht Raum für eine Integration beider Ansätze😉.

Zuerst zu den Grundlagen von Quantum Cognition. Quantum Cognition benutzt drei Schlüsselelemente der Quantenmechanik:

Superposition (Überlagerung): Ein mentaler Zustand kann als Kombination mehrerer möglicher Zustände betrachtet werden. Damit eröffnet sich die Möglichkeit, Ambiguitäten im menschlichen Verhalten zu modellieren, sowie Unentschlossenheit in Entscheidungsprozessen zu beschreiben.
Nicht-Kommutativität (Interferenz): Wie in der Quantenphysik können mentale Zustände sich gegenseitig beeinflussen, was zu Verstärkungs- oder Abschwächungseffekten führt und einige nichtlineare Entscheidungsprozesse erklärt. Psychologische Beispiele hierfür sind das Priming und die verschiedenen mentalen Verzerrungen, u.a. auch der Bias.
Verschränkung (Entanglement): Unterschiedliche kognitive Variablen können stark miteinander verbunden sein, so dass der Zustand einer Variablen unmittelbar den Zustand einer anderen beeinflusst. Das Hebb’sche Gesetz beschreibt diesen Effekt: Psychologische Beispiele hierfür sind Gefühle, die unmittelbar die Wahrnehmung beeinflussen.

Ich habe diese drei Schlüsselelemente in den Abbildungen 1-3 skizziert. Die in diesen Abbildungen enthaltenen mathematischen Ausdrücke der Quantenmechanik sind meines Erachtens nicht wichtig für ein Verstehen der wesentlichen Aussagen dieses Blog-Beitrages. Sie mögen aber dem ein oder anderen vielleicht beim besseren Verständnis helfen.

Ich erläutere im Folgenden die in Abbildung 2 enthaltenen Aussagen zum Schlüsselelement der Nicht-Kommutativität (Interferenz) etwas genauer, u.a. deswegen weil dort der Begriff des Projektionsoperators eingeführt wird, der für die Quantenmechanik und die Quanten Cognition von großer Bedeutung ist. Für die beiden anderen Schlüsselelemente verweise ich auf die Abbildungen 1-3.

Wenn wir an eine Person oder an ein Ding denken, so rufen wir ein mentales Konzept von dieser Person oder diesem Ding ab. Nehmen wir zwei Personen aus der amerikanischen Politik: Clinton und Gore. Jeder von uns hat wahrscheinlich ein mehr oder weniger ausgeprägtes Konzept bzw. eine mentale Repräsentation oder eine Idee von Clinton und Gore. Dieses Konzept wird u.a. durch Interaktion mit der Umwelt aktiviert. In unserem Clinton-Gore-Beispiel sind Konzepte wie ‚Clinton‘ und ‚Gore‘ die grundlegenden Einheiten, die wir modellieren möchten: Nehmen wir an, jemand würde uns die Frage stellen, ob wir Clinton vertrauenswürdig finden und anschließend die Frage stellen, ob wir Gore vertrauenswürdig finden. Psychologische Experimente haben gezeigt, dass die Wahrscheinlichkeit, beide Fragen mit Ja zu beantworten auch von der Reihenfolge der Fragen abhängt [3]. D.h. die Fragen rufen Konzepte auf und die Konzepte beeinflussen sich gegenseitig, aber nicht-kommutativ. Nicht-kommutativ bedeutet, dass es auf die Reihenfolge der Fragestellung ankommt. – Ein sehr erstaunliches Phänomen. In der Welt der Quanten kennt man entsprechende Phänomene: Die Reihenfolge von Messungen hat Einfluss auf die Ergebnisse der Messungen.

In der Quantenmechanik verwendet man sogenannte Projektionsoperatoren, die eine Messung bzw. Messreihenfolge repräsentieren. Mit einem Projektionsoperator projiziert man den Ausgangszustand auf den gemessenen Zustand. Damit kann man Wahrscheinlichkeitsaussagen treffen, wie wahrscheinlich es ist, dass der Ausgangszustand in den gemessenen Zustand übergeht.

Entsprechend werden in der Quantum Cognition kognitive Projektionsoperatoren zur Modellierung der Aktivierung eines kognitiven Konzepts in einer Person benutzt. – Es findet sozusagen eine Messung statt.

Nehmen wir an, dass bei der Frage nach Clinton bei einer befragten Person eine gewisse Ambivalenz (vertrauenswürdig, nicht-vertrauenswürdig) bezüglich der Antwort vorhanden ist. Für Gore nehmen wir eine andere Ambivalenz an. Wir nehmen auch an, dass bevor die Fragen gestellt werden, es noch keine Manifestationen von Präferenzen gibt. – Es gibt zum Beispiel keinen Bias durch eine gerade stattgefundene Diskussion zu diesem Thema. Die Projektionsoperatoren konstruieren wir als ambivalente Mischung (Superposition) aus einem vertrauenswürdigen und einem nicht-vertrauenswürdigen Basiskonzept. Hierbei kann es durchaus sein, dass eine befragte Person Clinton in dieser ambivalenten Mischung für vertrauenswürdiger als nicht-vertrauenswürdig hält. Bevor die Frage gestellt wird, ist dies jedoch nicht sichtbar, die innere Haltung ist unentschieden. Entsprechendes gilt natürlich für eine andere ambivalente Mischung bei Gore.

In der Quantenmechanik bezeichnet man die Basiskonzepte als Vektoren im sogenannten Hilbertraum. Der Hilbertraum ist ein spezieller mathematischer Raum, in dem die Vektoren quantenmechanischen Operationen unterliegen. Die Projektionsoperatoren sind solche Operationen und werden als Tensoren (haben das Aussehen von Matrizen) beschrieben, die auf diese Vektoren wirken. – Tensoren sind auch die zentralen Operationen in klassischen AI-Systemen. – Im Quanten Computing implementieren die Qubits die Vektoren und die Wechselwirkung der Vektoren entsprechen den Tensoren.

Wendet man den Formalismus der Quantenmechanik an, so kann man zeigen, dass nicht-kommutative Projektionsoperatoren, angewendet auf ambivalente innere Haltungen, eine Interferenz in den Antworten erzeugen. Die Basiskonzepte ‚Clinton‘ und ‚Gore‘ interferieren wie Wellen in der Physik: U.a. interferiert das vertrauenswürdige Basiskonzept mit dem nicht-vertrauenswürdigen Basiskonzept. Dies führt auch dazu, dass die Reihenfolge der Fragen entscheidend ist, da in Abhängigkeit der Reihenfolge unterschiedliche Interferenzen auftreten. Dies bedeutet, dass die gemeinsame Wahrscheinlichkeit Clinton zuerst als vertrauenswürdig einzustufen und anschließend Core, verschieden ist von der gemeinsamen Wahrscheinlichkeit Core zuerst als vertrauenswürdig einzustufen und anschließend Clinton. – Magisch…jedoch genau solche Effekt werden tatsächlich gemessen:

Wird zuerst nach Clinton als vertrauenswürdig gefragt und dann nach Gore, ergibt sich im statistischen Mittel, dass 50% der Befragten Clinton für vertrauenswürdig halten, und 68% Gore. Stellt man die Reihenfolge um, so geben 60% Gore als vertrauenswürdig an und 57% Clinton [3]. Es entsteht also eine Diskrepanz von ca. 7-8 %, hervorgerufen durch die Reihenfolge. Mit Hilfe der Formeln in Abbildung 2 zu den Wahrscheinlichkeiten lassen sich die Wahrscheinlichkeiten P _{Clinton dann Gore} = 0,340 und P _{Gore dann Clinton} = 0,342 berechnen. Die gemessenen Wahrscheinlichkeiten sind klassische statistische Wahrscheinlichkeiten, enthalten also Aussagen zu einer mittleren mentalen Ambivalenz aller befragten Personen. Berücksichtigt man dies, so kann man mit Hilfe des quantenmechanischen Formalismus Aussagen über die mittlere Ambiguität und Interferenz der mentalen Konzepte treffen:

In der Sequenz ‚Clinton dann Gore‘ zeigen die Berechnungen, dass weniger Ambiguität bezüglich Gore vorliegt, wenn zuerst nach Clinton gefragt wird. Dies deutet darauf hin, dass die mentale Repräsentation von Gore klarer oder positiver ist, wenn sie durch die vorherige Frage nach Clinton beeinflusst wird.

In der Sequenz ‚Gore dann Clinton‘ zeigen die Berechnungen, dass die Ambiguität bezüglich Clinton höher ist, wenn Gore zuerst gefragt wird. Dies deutet daraufhin, dass die mentale Repräsentation von Clinton stärker vom Kontext und vorherigen Informationen abhängt.

Abbildung 1: Superposition von mentalen Basiskonzepten

Abbildung 2: Nicht-Kommutativität und Interferenz von Basiskonzepten

Abbildung 3: Verschränkung von Basiskonzepten

Nach dieser kleinen Einführung in die Schlüsselelemente der Quantum Cognition, wende ich mich dem deutlich komplexeren Thema der Team-Kommunikation bzw. der Collective Mind Modellierung eines Teams zu.

Ich wollte hier ursprünglich ein Beispiel mit drei Teammitgliedern und den Big Five Persönlichkeitsmerkmalen, die einen Hilbertraum aufspannen, skizzieren. Jedoch haben die ersten Tests mit einem dazugehörigen Simulations-Programm auf einem klassischen Computer ergeben, dass dieses Programm schon nicht mehr auf meinem Laptop mit 16 GB Hauptspeicher lauffähig ist. Der Grund liegt darin, dass ein Hilbertraum mit 32768 Dimensionen aufgespannt wird. Die Dimension 32768 = 2 hoch (3*5), ergibt sich aus 3 Teammitglieder mit jeweils 5 Big Five Dimensionen. Jede Big Five Dimension wird durch einen Zustand 1 (hohe Ausprägung) und 0 (niedrige Ausprägung) repräsentiert. Es werden also für die Beschreibung der Wechselwirkung der Personen Tensoren (Matrizen) benötig, die eine Größe 32768*32768 haben.

Statt dessen skizziere ich hier ein Beispiel aus 3 Teammitgliedern und lediglich 2 Big Five Dimensionen, nämlich Offenheit und Gewissenhaftigkeit. Damit wird ein Hilbertraum von 64 Dimensionen aufgespannt. Die Berechnungen hierzu liegen im Sekundenbereich.

Die drei Teammitglieder nenne ich Alice, Bob und Charlie. Diese Namen sind Klassiker in jeder Literatur über Quantenmechanik.

Ich wähle als Start für meine Berechnungen folgende Big Five Dimensionen:

	Offenheit	Gewissenhaftigkeit
Alice	hoch	unbestimmt
Bob	unbestimmt	hoch
Charlie	unbestimmt	niedrig

Tabelle 1: Ausgangszustände der Big Five Dimensionen der Teammitglieder Alice, Bob und Charlie

Ein Zustand, der als hoch bezeichnet wird, startet mit einer Qubit ‚1‘. Ein Zustand, der als niedrig bezeichnet wird, startet mit einer Qubit ‚0‘ und ein unbestimmter Zustand wird als Superposition der Zustände hoch und niedrig modelliert. Abbildung 4 enthält diese Aussagen in einer etwas formalisierten Form.

Abbildung 4: Anfangszustände und Interaktionsoperator im Teammodell

Da wir 2 Big Five Dimensionen für 3 Teammitglieder haben, benötigen wir 6 Qubits. Wir führen keine Berechnung auf einem Quantencomputer durch, sondern arbeiten mit einer Quantensimulation, also mit einer quantenmechanischen Berechnung, durchgeführt auf einem klassischen Computer, meinem Laptop.

Diese Berechnung soll folgende Fragenstellungen untersuchen:

Wie hoch ist die Wahrscheinlichkeit, dass alle Mitglieder eine hohe Offenheit aufweisen, obwohl nur Alice dies als Präferenz mitbringt?

Wie hoch ist die Wahrscheinlichkeit, dass alle Mitglieder eine hohe Gewissenhaftigkeit aufweisen, obwohl nur Bob dies als Präferenz mitbringt?

Wie hoch ist die Wahrscheinlichkeit, dass sich das System in einem Collective Mind Zustand befindet und zwar in zwei Varianten. Variante 1: alle Offenheit-Qubits sind verschränkt. Variante 2: alle Offenheit-Qubits und alle Gewissenhhaftigkeits-Qubits sind verschränkt.

Wir definieren wieder einen Projektionsoperator, der in diesem Fall ein Interaktionsoperator ist und nehmen der Einfachheit hier an, dass lediglich gleiche Big Five Dimensionen der Teammitglieder miteinander wechselwirken. Dies ist keine grundsätzliche Einschränkung, sondern ist lediglich der schon recht hohen Komplexität geschuldet. Abbildung 4 zeigt die wesentlichen quantenmechanischen Gleichungen.

Der Interaktionsoperator modelliert die Tendenz von Personen, sich aufgrund von Ähnlichkeiten in ihren Merkmalen zu beeinflussen. Wenn zwei Personen ähnliche Zustände für ein Merkmal haben, verstärkt der Operator diese Ähnlichkeit durch die Interaktion.

Wir können auf dieser Basis Wahrscheinlichkeiten für den Übergang aller Teammitglieder zu hoher Offenheit bzw. hoher Gewissenhaftigkeit berechnen. Damit können wir zwei der oben gestellten Fragen beantworten.

Um die dritte Frage zu beantworten, wie wahrscheinlich ist das Eintreten eines Collective Mind (CM), ist es wieder nötig entsprechende Projektionsoperatoren für Variante 1 und Variante 2 der Verschränkung zu bilden.

Dieser Collective Mind Operator projiziert ausgehend vom vorher berechneten Interaktions-Zustand auf einen Zustand maximaler Verschmelzung der individuellen Zustände zu einem gemeinsamen Bewusstsein.

CM Variante 1: Alle Qubits sind verschränkt. Dies repräsentiert einen Zustand, in dem alle Personen in Bezug auf beide Persönlichkeitsmerkmale vollständig synchronisiert sind.

CM Variante 2: Nur die Offenheits-Qubits sind verschränkt. Lediglich die Dimension Offenheit ist verschränkt, während Gewissenhaftigkeit variiert.

Abbildung 5 zeigt die quantenmechanischen Collective Mind Projektionsoperatoren für Variante 1 und 2.

Abbildung 5: Die Collective Mind Operatoren zu Variante 1 und 2

Nun zu den Ergebnissen: Das recht komplexe Python Programm für die Colab Umgebung wurde mit der AI-Assistenz von ChatGPT 4o1-preview erstellt. Hierbei wurde die Quantum Toolbox QuTIP [6] für die quantenmechanischen Tensor-Operationen verwendet.

Die modellierten Ergebnisse entsprechen qualitativ meinen Erfahrungen in Teams:

Die Ausbildung von einer Team-Präferenz für eine der Big Five Dimensionen hängt von der Reihenfolge der Interaktionen im Team ab: Je nachdem wer zuerst spricht entwickelt sich eine unterschiedliche Dynamik. Es ist von Vorteil, wenn zuerst Personen mit ähnlichen Präferenzen die Kommunikation starten. Sie unterstützen selbst dann Team-Präferenzen, wenn sie selbst keine Präferenz darin haben.

Die Wahrscheinlichkeit für eine Team-Präferenz Offenheit ist moderat, also nicht oberhalb von 50%, wenn nur eine Person diese als persönliche Präferenz hat.

Falls die Präferenz Gewissenhaftigkeit in einem Team durch eine Person vorhanden ist, kann es sein, dass sich die Team-Präferenz Offenheit in einem Team überhaupt nicht ausprägt.

Falls die persönliche Präferenz Gewissenhaftigkeit nur einmal (oder auch mehrmals, gemäß meiner Erfahrung) im Team vorhanden ist, ist die Wahrscheinlichkeit groß, dass sich keine Team-Präferenz Gewissenhaftigkeit ausbildet.

Abbildung 6 zeigt ein Beispiel für ein Szenario, in dem ich die weiter oben angegebenen persönlichen Präferenzen der Teammitglieder für Szenario 4 verändert habe: Die Präferenz Offenheit bleibt wie oben angegeben, jedoch setze ich die Präferenz Gewissenhaftigkeit für alle Teammitglieder auf ‚unbestimmt‘. Das erstaunliche hier ist, dass sich eine gewisse Wahrscheinlichkeit für eine Team-Präferenz Gewissenhaftigkeit ausbildet, obwohl keines der Teammitglieder diese Präferenz hat. In anderen, hier nicht gezeigten Szenarien, führt schon eine persönliche Präferenz Gewissenhaftigkeit immer zu einer sehr geringen Team-Präferenz Gewissenhaftigkeit. Auch dies entspricht meiner Erfahrung.

Abbildung 6: Die Wahrscheinlichkeiten zur Ausbildung der Team-Präferenzen Offenheit und Gewissenhaftigkeit in Abhängigkeit der Interaktionsreihenfolge. Die persönlichen Präferenzen Offenheit von Alice, Bob und Charlie entsprechen den ursprünglich festgesetzten. Die persönlichen Präferenzen Gewissenhaftigkeit für alle drei Personen wurde für dieses Szenario auf unbestimmt gesetzt.

Abbildung 7 zeigt für das Szenario 4 aus Abbildung 6 die Wahrscheinlichkeiten der Ausbildung eines Collective Mind für die Varianten 1 und 2. Die Wahrscheinlichkeit der Ausbildung eines Collective Mind für die Variante 1 (Offenheit und Gewissenhaftigkeit verschränkt) ist deutlich geringer als für Variante 2 (nur Offenheit verschränkt). Die Ausbildung des Collective Mind hängt auch ein wenig von der Interaktionsreihenfolge ab. Jedoch ist diese Abhängigkeit sehr gering: Wenn sich überhaupt ein Collective Mind ausbildet, so hat die Interaktionsreihenfolge kaum noch Einfluss darauf.

Abbildung 7: Die Wahrscheinlichkeiten zur Ausbildung eines Collective Mind für die Varianten 1 (Offenheit und Gewissenhaftigkeit sind verschränkt) und Variante 2 (nur Offenheit ist verschränkt).

Zusammenfassend stelle ich fest:

Der Quantum Cognition Formalismus liefert keine unsinnigen Ergebnisse. Im Gegenteil: Die Ergebnisse decken sich qualitativ mit meinen Erfahrungen. Ich finde die qualitative Interpretation der Ergebnisse erstaunlich nahe an der Praxis: So nahe, dass es schon sehr an Magie grenzt.

Der Nachteil ist, dass der Quantum Cognition Formalismus sehr anspruchsvoll ist. Ohne die AI-Assistenz von ChatGPT4o1-preview wäre es mir nicht möglich gewesen, diese Berechnungen durchzuführen. ChatGPT4o1-preview strauchelte auch einige Male. – Gemeinsam war es jedoch gut möglich dies aufzufangen.

Die Übertragung der Berechnungen auf ein QC Hardware System würde es erlauben, Teamgrößen von 7-10 Teammitgliedern zu modellieren. – Jedoch ist dies ein deutlicher Schritt in Richtung Komplexität, der es aber eventuell wert sein könnte.

[1] Wikipedia (2024a) Quantum Cognition, https://en.wikipedia.org/wiki/Quantum_cognition

[2] Brody D C (2023) Quantum formalism for the dynamics of cognitive psychology, https://www.nature.com/articles/s41598-023-43403-4

[3] Pothos E M und Busemeyer J R (2022) Quantum Cognition, Annual Review of Psychology, https://www.annualreviews.org/content/journals/10.1146/annurev-psych-033020-123501

[4] Wikipedia (2024b) Quantum Mind, https://en.wikipedia.org/wiki/Quantum_mind

[5] Oswald A, Köhler J, Schmitt R (2018) Project Management at the Edge of Chaos, Springer, Heidelberg

[6] QuTIP (2024) QuTIP Quantum Toolbox in Python, https://qutip.org/