Kurzfassung: Der Beitrag beschreibt, wie sich eine Aktien Portfolioauswahl als Optimierungsproblem formulieren lässt: Ein Bitstring codiert, welche Titel im Portfolio sind, und eine Zielfunktion balanciert Risiko gegen erwartete Rendite. Darauf aufbauend werden zwei Quantenwege gegenübergestellt: Quantum Annealing (z. B. D-Wave) liefert durch einen kontinuierlichen Übergang von Exploration zu Problem schnell viele Kandidatenportfolios als Samples, während QAOA im Gate-Modell über einen parametrierten Schaltkreis Interferenz nutzt, um gute Bitstrings wahrscheinlicher zu machen. Beide Methoden suchen nicht magisch die perfekte Lösung, sondern erkunden denselben Lösungsraum mit unterschiedlichen physikalischen Mechanismen und Auswerteformen. Der Text argumentiert, dass Quantum Computing weniger als Rechnen im klassischen Sinn verstanden werden kann, sondern eher als kollektiver Interferenz- und Resonanzprozess, der Strukturen im Lösungsraum verstärkt.
Dieser Beitrag, inklusive obiger Abbildung, wurde mit Hilfe von ChatGPT erstellt.
Ich beschäftige mich in diesem Blog-Beitrag mit der ‚Optimierung von Aktien Portfolios mittels Quantum Computing‘. Ein LinkedIn-Beitrag zum gleichen Thema brachte mich auf auf diese Idee [1].
Ziel dieses Blog-Beitrages ist es, die verschiedenen Quantum Computing Methoden aufzuarbeiten und soweit sinnvoll und machbar an dem Beispiel der Aktien Portfolio Optimierung auszuprobieren.
Wie meine Blog-Artikel der letzten Jahre zeigen, wende ich Quantum Computing (QC) in verschiedenen Facetten an: Quantum Cognition in der Entscheidungsfindung, Quantum Collective Mind in der Teambildung und Quantum Spiral Dynamics in der Kulturtransformation und der Demokratieanalyse.
Quantum ‚Computing‘ ist als Begriff etwas irreführend, weil er suggeriert, dass ein Quantencomputer wie ein klassischer Computer Schritt für Schritt auf der Basis von Zahlen Zwischenresultate produziert. Im sogenannten QC Gate-Modell passiert jedoch etwas anderes: Ein Quantenzustand wird über viele Quanten Schaltkreise (Quantum Gates) hinweg kohärent weiterentwickelt. Relevant ist z.B. nicht ‚ein Wert nach Gate Nr. 37‘, sondern das Interferenzmuster, das sich über die gesamte Schaltung aufbaut.- QC ist also ganzheitlich ausgelegt. Mathematisch gibt es zwar Zwischenzustände nach jeder Teiloperation, aber ohne Messung sind das keine lesbaren ‚Zwischenergebnisse‘ im klassischen Sinn – jede Messung würde die Dynamik verändern und damit genau die Kohärenz zerstören, auf der der Vorteil beruht. Das Ergebnis liegt daher typischerweise als Ganzes am Ende vor; nämlich als Messstatistik, die bestimmte Bitstrings oder Energien wahrscheinlicher macht als andere. In diesem Sinne ist Quantenrechnen weniger „Rechnen wie gewohnt“, sondern eher eine Form von kohärenter Informationsverarbeitung, bei der viele Pfade gleichzeitig durchlaufen und am Ende durch Interferenz verstärkt oder ausgelöscht werden. Ein Begriff wie „collective interference“ trifft diesen Kern besser.
QC ist universell: In allen QC Verfahren wird der sogenannte Hamiltonian, eine Funktion bzw. ein Operator, der die Energie eines Systems modelliert, verwendet. Jede mathematische Problemstellung lässt sich sich prinzipiell über einen Hamiltonian ausdrücken. Prinzipiell heißt in diesem Fall, dass es möglich ist, aber nicht immer sinnvoll ist, da die Umsetzung extrem schwierig sein kann. Für physikalische Fragestellungen ist der Hamiltonian immer geeignet und oft auch die eleganteste Form der Problemstellung: Es wird nach der niedrigsten Energie in einer Energielandschaft, ähnlich einer Gebirgslandschaft, gesucht. Die niedrigste Energie in einer Energielandschaft ist oft der ‚Aufenthaltsort‘ natürlicher Systeme.
Es gibt aber auch eine große Anzahl an klassischen Problemen, für die die Formulierung eines Hamiltonian einfach und elegant ist. Zum Beispiel gehören dazu: u. a. Aktion Portfolio Optimierung, Logistische Optimierungen oder Ressourcenoptimierung im Projektmanagement. In diesen Fällen wird das klassische Optimierungsproblem auf ein quantenmechanisches Optimierungsproblem transferiert und mittels QC nach dem Zustand gesucht, der die niedrigste Energie hat. Dieser Zustand repräsentiert die Lösung für das klassische Optimierungsproblem. Sind die Datenmengen gering, so ist der Einsatz von QC nicht nötig, steigen die Datenmengen so ist QC skalierbar; klassische Verfahren sind dies oft nicht mehr. Ich arbeite für die Aktien Portfolio Optimierung mit einer kleinen Watchliste von 20 Aktien und möchte daraus ein optimiertes Aktienportfolio von 4 Aktien erstellen. Selbst klassische Verfahren haben hiermit kein Problem und für die QC Methoden, die ich vorstelle, liegen die Simulationen auf einem gut ausgestatteten Laptop (also ohne QC Hardware) typischer Weise im Rechenzeit-Bereich von Minuten bis ca. einer Stunden. – Eine solche Problemstellung benötigt also noch nicht einmal eine QC Simulation auf einem klassischen Computer geschweige denn eine QC Hardware. Würden wir aber zum Beispiel 2000 Aktien in die Watchliste aufnehmen und wollten die 20 besten Aktien auswählen, sähe die Situation völlig anders aus: Falls wir keine Vorauswahl unter den 2000 Aktien treffen, müssten 10 hoch 47 Möglichkeiten überprüft werden. Dies ist außerhalb jeglicher klassischer Möglichkeiten. Ab einer Watchliste von ungefähr 60-70 Aktien sind klassische Verfahren ungeeignet.
Auch QC Hardware Systeme erlauben heute noch nicht solche Fragestellung zu behandeln, da mindestens 2000 Qubits (eher viel mehr) notwendig sind, um die klassische Fragestellung in eine QC Fragestellung umzusetzen. – Jedoch gibt es einen wesentlichen Unterschied: QC Methoden haben keine prinzipielle Schranke und sobald fehlertolerante QC Hardware vorhanden ist, können auch solche Fragestellungen beantwortet werden. Es gibt schon heute QC Hardware-Systeme, die für viele Optimierungsprobleme gut geeignet sind, nämlich die sogenannten Annealing Optimierer von D-Wave. Man siehe auch meine vergangenen Blog-Beiträge, in denen ich diese Systeme benutzt habe [2, 3, 4].
QC Methoden sind also in Bereichen skalierbar, in die klassische Methoden prinzipiell nicht vordringen können! – Die Beschäftigung mit diesen Methoden ist deshalb auch heute schon sinnvoll: QC wird in naher Zukunft zusammen mit AI Wissenschaft und Innovation revolutionieren.
Quanten Computing kennt aktuell vier verschiedene Methoden, drei davon basieren auf Quanten Schaltkreisen und eine auf Adiabatischer Optimierung. – Ich verweise auch auf die Anhänge 1 und 2 mit einer tabellarischen Übersicht zu den vier Methoden, einem kleinen Glossar und einer Methoden Formelsammlung:
QAOA (Quantum Approximate Optimization Algorithm)
QAOA ist eine Gate-Methode für Optimierungsprobleme, bei der eine Zielfunktion in einen Hamiltonian umgesetzt wird und eine Energie Verteilung nach Wahrscheinlichkeiten ermittelt wird. Die wahrscheinlichste und niedrigste Energie repräsentiert die Lösung. Jede Lösung wird als Bitstring (0/1-Folge) dargestellt, z. B. „Asset gewählt“ = 1, „nicht gewählt“ = 0. QAOA baut einen Quanten-Schaltkreis aus wiederholten Schaltkreis Blöcken. Jeder Block enthält einen Problem-Schritt, der gute Lösungen bevorzugt, und einen Misch-Schritt, der hilft, in möglichst der gesamte Energielandschaft nach der niedrigsten Energie zu suchen.
Die einstellbaren Optimierungsparameter sind Winkel in sogenannten Rotationsgattern, z. B. dreht ein Gate den Qubit-Zustand entlang einer Achse (x-, y- Achse) um einen Winkel. – Dies erzeugt einen neuen Zustand und damit eine Bewegung innerhalb der Energielandschaft. Eine klassische Optimierungsschleife probiert Parameterwerte aus und verbessert sie so, dass beim Messen möglichst häufig tiefe Energien, also ‚gute‘ Bitstrings, auftreten. Meistens ist es notwendig, den Quanten Schaltkreis mehrmals hintereinander zu setzen. Man spricht von Schaltkreis-Schichten, die das Ergebnis verbessern.
VQE (Variational Quantum Eigensolver)
VQE ist eine Gate-Methode und wird genutzt, um für ein gegebenes Modell (oft ein physikalischer Hamiltonian) den Grundzustand zu finden. Der Grundzustand ist der Zustand mit der niedrigsten Energie. Man wählt für den Hamiltonian eine parametrisierte Ansatz Schaltung: Mit einstellbaren Parametern (wieder häufig Rotations-Winkel) werden möglichst viele Zustände erzeugt.
Eine klassische Optimierungsschleife verändert die Ansatz Parameter so lange, bis die gemessene Energie minimal wird. VQE ist besonders attraktiv auf heutiger Hardware, weil es keine extrem langen Schaltkreise voraussetzt.
QPE (Quantum Phase Estimation)
QPE ist eine Gate-Präzisionsmethode, um Eigenwerte (z. B. Energien) eines Hamiltonians zu bestimmen. Man betrachtet hierfür die Zeitentwicklung eines sogenannten Eigenzustandes (U=e^{-iHt}). Wenn ein Zustand ein Eigenzustand ist, bekommt er unter U nur eine Phase (eine Art „Drehwinkel“ im komplexen Zahlenraum) – diese Phase hängt direkt mit der Energie zusammen.
QPE nutzt ein Zusatzregister, das Qubit Phasenregister, das am Ende eine Binärzahl enthält (z. B. 010101…), die die Energie kodiert. Dafür benötigt man kontrollierte Zeitentwicklungen und viele präzise Operationen. Darum ist QPE zwar theoretisch sehr stark, aber praktisch auf NISQ-Hardware meist schwierig, weil es sehr rauschempfindlich ist. Diese Methode ergänzt die anderen Methoden, denn es ist notwendig mit einem ‚guten‘ Eigenwert zu starten, um diesen dann sehr genau zu vermessen.
D-Wave / Quantum Annealing (Adiabatische Optimierung)
Die QC Methode Quantum Annealing basiert nicht auf Gates, sondern auf einem Qubit-Netzwerk: Die Qubits sind in dem Netzwerk ähnlich wie die atomaren Magnete eines Ferromagneten verbunden. Zuerst werden die Qubits mittels eines externen Magnetfeldes in einen ‚ferromagnetischen‘ Anfangszustand gebracht. Das externe Magnetfeld wird als Driver bezeichnet und hat eine ähnliche Funktion wie der Mixer in der QOAO-Methode: Mittels eines zeitlichen Fahrplans wird der Driver sehr langsam Schritt für Schritt (adiabatisch) ausgeschaltet und der Problem-Hamiltonian angeschaltet. Man nennt diesen Vorgang auch Annealing (in Analogie zum Abkühlen/Ausglühen bei klassischen Phasenübergängen).
In der Praxis wird der Annealing Prozess sehr oft durchgeführt. Man erhält typischerweise viele Samples: also viele gemessene Bitstrings mit den daraus ermittelten Energien und Häufigkeiten. Diese Informationen repräsentieren die Struktur der Energielandschaft.
Da man kein Qubit-Netzwerk aufbauen kann, in dem jedes Qubit mit jedem verbunden ist, muss man Kompromisse schließen: Dieses sogenannte Embedding sollte möglichst gut zur Optimierungsaufgabe passen. Weil die Hardware eine feste Verbindungsstruktur hat, werden oft Problemanforderungen durch mehrere physikalische Qubits als „Kette“ repräsentiert. Sieht man von diesen Hardwareproblemen ab, so ist die Adiabatische Optimierung schon heute für viele (klassische) Optimierungsprobleme einsetzbar [5].
Da die Aktien Portfolio Optimierung kein quantenmechanisches System darstellt, sondern eine klassische Problemstellung, entfallen die beiden Methoden VQE und QPE und es bleiben für die Aktien Portfolio Optimierung die beiden Methoden QAOA und Quantum Annealing übrig. Mittels ChatGPT implementiere ich QAOA für das IBM System Qiskit [6] und Quantum Annealing für das D-Wave System [5].
Ich habe für diesen Blog lediglich 20 Assets ausgewählt und möchte aus diesen 20 Assets die 4 Assets auswählen, die das geringste Risiko und die höchste Rendite ergeben. Ich nehme der Einfachheit für diesen Blog an, dass alle Assets mit gleichen Gewichten in das Portfolio eingehen.- Eine Erweiterung auf ungleiche Gewichte könnte ein Thema für einen weiteren Blog sein.
Ich verwende Kurs Daten der letzte 252 Tage von yahoo finance. Die Rendite bzw. die Kurse der Assets gehen als lineare Terme in den Hamiltonian ein. Zusätzlich wird aus den yahoo finance Daten eine Kovarianzmatrix ermittelt, die die Risiken und deren Abhängigkeiten abbildet. Der Hamiltonian wird sowohl für das QAOA Modell als auch für das Quantum Annealing Modell in ein Ising Modell transformiert. Im Ising Modell geht die Kovarianzmatrix in die Paar-Kopplungsmatrix Jij über (man siehe hierfür die Formeln Anhang 2).
Die nachfolgende Tabelle 1 enthält die ausgewählten Assets:
| Asset Kürzel | Beschreibung (.Börse) |
| AAPL | Apple |
| AMZN | Amazon |
| GOOGL | |
| NVDA | Nvidia |
| QBTS | D-Wave Quantum |
| ^DJI | Dow Jones |
| ^GDAXI | DAX |
| ^IXIC | NASDAQ |
| MSF.DE | Microsoft. Deutschland |
| ^MDAXI | MDAX |
| ^TECDAX | TECDAX |
| RHM.DE | Rheinmetall AG. Deutschland |
| EOS.AX | Electro Optics Systems Holding. Australien |
| DRH.F | DroneShield. Frankfurt |
| MBB.DE | MBB SE. Deutschland |
| RGTI | Rigetti Computing |
| OBCK.DU | Ottobruck SE. Düsseldorf |
| IONQ | IonQ |
| 5Q5.DE | Snowflake. Deutschland |
| ASM.F | ASML Holding. Frankfurt |
Tabelle 1: Liste der Watchlist-Assets mit Daten von yahoo finance, die über die Python Funktion yfinance geladen werden. Die zum Zeitpunkt der Ausführung des Programms rückwirkend verfügbaren 252 Daten pro Asset werden verwendet. Falls nicht genug Daten für ein Asset vorliegen, wird dieses Asset in dem QC nicht berücksichtigt. Zum Zeitpunkt der im Blog durchgeführten Berechnungen waren für die Assets OBCK.DU und ASM.F nicht genügend Daten vorhanden. Ich habe die Watchliste trotzdem nicht verändert, da der Blog keine Finanzberatung darstellt, und zu einem späteren Berechnungs-Zeitpunkt dieser Ausschluss automatisch wegfällt.
Nun zu den Ergebnissen:
IBM QAOA mit 2 Schaltkreis-Schichten (p = 2)
Die 2 Schaltkreis Schichten führen insgesamt zu einem gewaltigen Schaltkreis von 35 nebeneinander gelegten DIN A4 Seiten. Das führt in der Simulation zu Rechenzeiten von mehr als einer Stunde auf meinem Laptop.
Das Ergebnis ist nicht wirklich gut: Die wahrscheinlichsten Energien sind positiv: Diese Energien sind also Berggipfel. Es gibt eine negative Energie, jedoch mit geringer Wahrscheinlichkeit: Das so ermittelte ‚gute‘ Portfolio besteht aus Apple, Google, RHM.DE und MDAXI mit einer prognostizierten Jahresrendite von 65% und einer Volatilität von 20%. Dieses Ergebnis stimmt nicht mit dem D-Wave Ergebnis überein und ist deutlich schlechter als dieses.
D-Wave Quantum Annealing
Die Quantum Annealing Simulation ist schlank, was sich in einer Rechenzeit von ca. 10 Minuten auf meinem Laptop niederschlägt. Es wird ein Energieminimum gefunden, das sehr nahe am Ergebnis einer Brute Force Berechnung liegt. Die Brut Force Methode schlägt als Portfolio folgende Assets vor: EOS.AX, Google, MBB.DE, RHM.DE. Das Quantum Annealing ermittelt: Google, MBB.DE, RHM.DE, ^DJI. Dieses Portfolio hat eine prognostizierte Jahresrendite von 95% und eine Volatilität von 23%.
Selbst eine intensive Suche nach Ursachen für das ‚schlechte‘ Resultat der QOAO Methode brachte keine Ergebnisse. – Die KI-Systeme Claude und Mistral als Qualitätssicherer erzeugten zwei ‚korrigierte‘ Programme, die völlig unsinnige Resultate lieferten.
Eine QC Simulation auf meinem Laptop für das QAOA Programm mit mehr als 2 Schichten steigert die Rechenzeit nochmals merklich, so dass ich diese abbrach. Ein erster Test auf der IBM Hardware mit einem geschenkten Budget von 10 Minuten (die Kosten betragen aktuell ca. 20 Euro/Sekunde!) brachte eher Frustration: Die IBM-Infrastruktur kennt wieder Jobs, wie vor Jahrzehnten. D.h. auch, die QC Software, die man für die Simulation verwendet, kann nicht ohne (größere) Änderungen für die Hardware verwendet werden. Da ich dies nicht wusste, war mein Budget ohne Ergebnis im Handling zwischen QC Hardware und klassischer Hardware ‚verschwunden‘.
Diese Ergebnisse sind sicherlich nicht perfekt, jedoch zeigen sie Potential für weitere Blog-Beiträge!
[1] Dominika Pillerova https://www.linkedin.com/feed/update/urn:li:activity:7390849746438955009?utm_source=share&utm_medium=member_ios&rcm=ACoAAADwjS8Blpat6RQsfTtvnIu1lnZS6K7fuLk
[2] AI & QC & M 4.0: Alles Quantum? oder von Quantum Computing Modell-Archetypen, Dezember 2024,
https://agilemanagement40.com/ai-qc-m-4-0-alles-quantum-oder-von-quantum-computing-modell-archetypen
[3] AI & QC & M 4.0: Quantum Cognition für das Team-Management oder von der Macht der Mathematik, Oktober 2024,
https://agilemanagement40.com/ai-qc-m-4-0-quantum-cognition-fuer-das-team-management-oder-von-der-macht-der-mathematik
[4] AI & QC & M 4.0: Die Welt der Unbestimmtheit nutzen oder vom Nutzen des Quantum Computing für das Team-Management, Oktober 2024,
https://agilemanagement40.com/ai-qc-m-4-0-die-welt-der-unbestimmtheit-nutzen-oder-vom-nutzen-des-quantum-computing
[5] D-Wave Quantum, www.dwavequantum.com
[6] IBM Qiskit, https://quantum.cloud.ibm.com/
Anhang 1
Kleines Glossar
Annealing/Quantum Annealing (D-Wave): Das System startet in einem leicht vorbereitbaren Zustand (Driver) und wird über einen Zeitplan zum Problem-Hamiltonian geführt, sodass am Ende möglichst niedrige Energien herauskommen.
Basiszustand (Ground State): Der Zustand mit der niedrigsten Energie eines Hamiltonians.
Bitstring: Ein Messergebnis als 0/1-Folge, z. B. 1010. In Optimierungsproblemen entspricht ein Bitstring oft einer Auswahlentscheidung („1 = gewählt, 0 = nicht gewählt“).
Constraint (Nebenbedingung): Eine Zusatzregel wie ‚genau x Aktien auswählen‘. Wird oft über Strafterm (Penalty) oder spezielle Mixer umgesetzt.
Chain (Kette): Mehrere physikalische Qubits, die gemeinsam eine logische Variable repräsentieren. Ketten können „brechen“, dann braucht man Nachbearbeitung.
Dekohärenz: Verlust von Quanteneigenschaften (Superposition/Phase) durch Wechselwirkung mit der Umgebung – „Welleninformation verwischt“.
Driver-Hamiltonian: Beim Annealing der Teil, der Exploration/Superposition erzeugt. Er wird im Zeitplan zugunsten des Problem-Hamiltonians zurückgefahren.
Embedding: Abbildung eines logischen Problems auf die feste Kopplungsstruktur der Annealer-Hardware, oft mit Ketten mehrerer Qubits pro Variable.
Erwartungswert: Statistischer Mittelwert einer Messgröße (z. B. mittlere Energie).
Fault-tolerant (fehlertolerant): Rechner kann lange Berechnungen zuverlässig ausführen, weil Fehler aktiv erkannt und korrigiert werden.
Fehlerkorrektur (Error Correction): Methoden, um logische Qubits gegen Fehler zu schützen; benötigt viele physikalische Qubits pro logischem Qubit.
Gate (Quanten-Gatter): Elementare Operation, die Amplituden und Phasen verändert – Baustein eines Quanten-Schaltkreises.
Hamiltonian (H): Mathematische Beschreibung der Energie eines Systems. In Optimierungen wird H so gebaut, dass niedrige Energie = gute Lösung.
Hamming-Gewicht: Anzahl der Einsen in einem Bitstring. Beispiel: 10110 hat Gewicht 3. Wichtig bei ‚wähle genau x Assets‘.
Hybrid-Algorithmus: Kombination aus Quanten-Teil und klassischem Teil (z. B. Quantenmessung + klassischer Optimierer bei QAOA/VQE).
Interferenz: Überlagerung von Wellenwegen: Manche verstärken sich, andere löschen sich aus. Das ist der Kern von Quantenalgorithmen.
Ising-Modell: Optimierungsform mit Spins (s_i, i ={+1,-1}), eng verwandt mit QUBO. Viele Quanten-Optimierer nutzen diese Darstellung.
Klassische Schleife (Optimierungsschleife): Wiederholtes Anpassen von Parametern durch einen klassischen Optimierer, basierend auf Messdaten (typisch bei QAOA/VQE).
Problem-Hamiltonian/Kosten-Hamiltonian: Der Hamiltonian, der die Zielfunktion kodiert (z. B. mittels Risiko und Rendite). Definiert, was „gut“ ist.
Messung (Measurement): Schritt, der aus dem Quantenzustand klassische 0/1-Ergebnisse macht. Für Wahrscheinlichkeiten braucht man viele Wiederholungen.
Mixer-Hamiltonian (QAOA): Teil des QAOA, der Zustände „durchmischt“, um Exploration zu ermöglichen (z. B. X- oder XY-Mixer).
NISQ (Noisy Intermediate-Scale Quantum): Heutige Gerätegenerationen sind noisy und damit noch nicht zuverlässig genug um tiefe Algorithmen abzubilden
Noise (Rauschen): Sammelbegriff für Fehlerquellen (Dekohärenz, Gate-Fehler, Messfehler), die die Berechnung verfälschen.
Output-Verteilung: Statt eines einzigen Ergebnisses erhält man eine Verteilung (Histogramm) über Bitstrings; gute Lösungen mit niedriger Energie sollten häufiger auftreten.
Parameter / Schaltkreis-Winkel: Einstellbarer Zahlenwert in Rotationsgattern (Drehwinkel). QAOA/VQE suchen die besten Werte.
Penalty (Strafterm): Zusätzliche Energie, die unerwünschte Lösungen teuer macht (z. B. falsche Anzahl gewählter Assets).
Phase: Winkel-Information eines Quantenzustands. Phasen steuern Interferenz und sind zentral für QC-Algorithmen.
Phasenregister: Zusatz-Qubits, in denen QPE eine Zahl (Phase/Energie) in Binärform speichert.
QUBO (Quadratic Unconstrained Binary Optimization): Optimierung mit binären Variablen (x_i in {0,1}) und quadratischen Kopplungen (x_i*x_j).
Schaltkreis (Quantum Circuit): Abfolge von Quanten Gattern, die Qubits verändern; am Ende wird meist gemessen.
Shots: Anzahl der Wiederholungen derselben Schaltung. Mehr Shots = bessere Statistik, aber höhere Kosten/Laufzeit.
Superposition: Ein Qubit kann gleichzeitig in Anteilen von 0 und 1 sein. Grundlage für paralleles Durchlaufen vieler Möglichkeiten.
Übersicht zu den vier QC Methoden
| Aspekt | D-Wave (Quantum Annealing) | QAOA | VQE | QPE |
|---|---|---|---|---|
| Typische Anwendungsbereiche | Kombinatorische Optimierung als QUBO/Ising (z. B. Portfolio-Auswahl, Scheduling, Routing, Zuordnungsprobleme), Sampling aus vielen ‚guten‘ Lösungen (Landschaft/Regime erkunden) | Kombinatorische Optimierung auf Gate-Hardware: ähnlich wie Quantum Annealing | Grundzustand-Suche / Energie-Minimierung für Modelle (Chemie, Materialien, kleine Hubbard-Modelle), auch als Optimierer nutzbar, wenn die Zielfunktion als Hamiltonian messbar ist | Präzise Eigenwert-/Spektralanalyse (Energien, Phasen), wichtig als Diagnose-Tool in der Theorie und bei fehlertoleranter Hardware (Chemie/Physik, langfristig auch QFT/Simulation) |
| Basis (Hardware) | Annealing (zeitabhängiger Hamiltonian) | Gate-Schaltkreis | Gate-Schaltkreis | Gate-Schaltkreis |
| Grundidee | Maschine fährt einen Zeitplan: von „Exploration“ (Driver) zu „Problemenergie“ (Ziel) | Wiederholt zwei Schritte: (1) Problemenergie „prägen“, (2) Zustände „mischen“ | Baue einen Probe-Zustand mit Parametern und minimiere die gemessene mittlere Energie | Lässt den Zustand unter H ‚laufen‘ und liest die Phase aus → Energie als Binärzahl |
| Wie das Problem modelliert wird | Direkt als Ising/QUBO-Energie auf der Hardware (plus Einbettung/Embedding) | Als Problem-Hamiltonian + Mixer-Hamiltonian als Schaltkreise | Als Hamiltonian H, dessen Erwartungswert gemessen wird | Als Zeitentwicklung (U=e^{-iHt}) |
| Rolle von Driver/Mixer | Driver erzeugt Exploration, ist aber im Zeitplan mit dem Problem ‚verblendet‘ | Mixer sorgt für Exploration (z. B. X- oder XY-Mixer) | Kein Mixer: Exploration kommt über die Ansatz-Familie + klassische Parameter-Suche | Kein Mixer: Fokus ist präzises Auslesen der Energie/Phase |
| ‚Zeit‘ im Algorithmus | Kontinuierlich (adiabatischer/ annealender Verlauf) | Diskret in Schichten (diskrete Annäherung an Annealing) | Keine physikalische Zeit nötig; nur Zustandspräparation + Messung | Explizite Zeitentwicklung ist zentraler Bestandteil |
| Braucht klassische Optimierung in der Schleife? | Nein: man macht viele Runs/Samples und wählt aus | Ja: klassische Optimierung der Schaltkreis-Parameter | Ja: klassische Optimierung der Ansatz-Parameter | Meist nein; ggf. Wiederholungen für Genauigkeit/ Parameterwahl |
| Was kommt am Ende raus? | Viele Bitstring-Samples + Energien/Häufigkeiten | Verteilung über Bitstrings (gute Lösungen häufiger) | Erwartungswerte, v. a. mittlere Energie | Energie als Binärzahl im Phasenregister (sehr präzise) |
| Stärken | Schnell viele Kandidaten; gut zum Erkunden einer komplexen Lösungslandschaft | Gute NISQ-Heuristik für Optimierung; Schaltkreis Annealing | Sehr nützlich für Grundzustände auf NISQ; flexibel über Ansatz | Höchste Präzision für Spektren, wenn Hardware fehlerarm ist |
| Schwächen | Embedding kann teuer sein; kalibrierungs-sensitiv | Viele Messungen/ Iterationen; Ergebnis ist heuristisch | Messaufwand; Ansatz kann „zu eng“ sein | Große Schaltkreistiefe; extrem rauschsensitiv (heute schwer) |
| Hardware-Anforderung | Spezial-Annealer | NISQ-Gate-Hardware | NISQ-Gate-Hardware | In der Praxis meist fehlertolerant nötig |
Anhang 2
Formeln der vier QC Methoden
Gemeinsame Basis (QUBO/Ising)
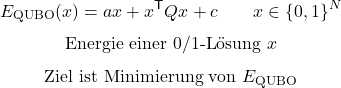
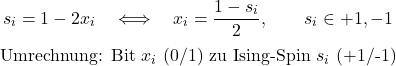
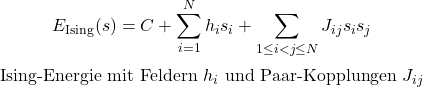
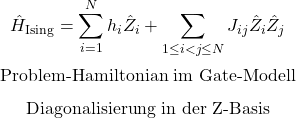
QAOA

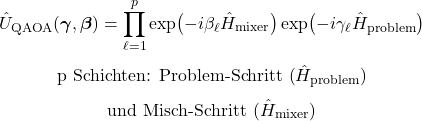
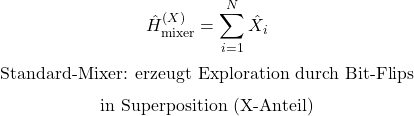



VQE

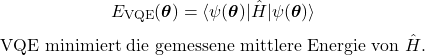


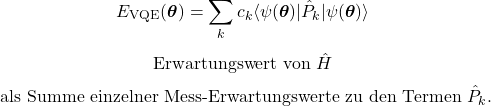
QPE
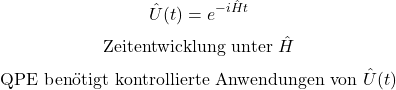
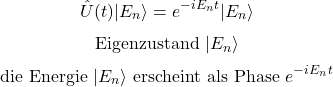
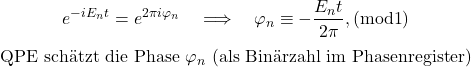
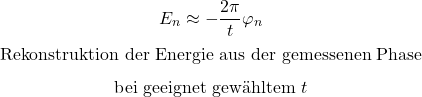
Quanten-Annealing (D-Wave / adiabatisch)
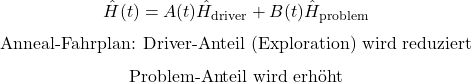

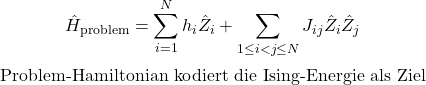
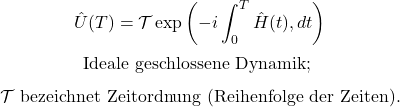
QAOA als Annäherung an eine Annealing-Dynamik
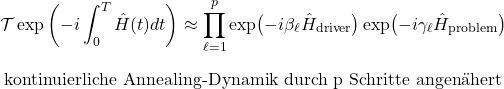
Zur unterschiedlichen Verwendung des Begriffes Annealing:
QAOA kann man als ‚Schaltkreis-Annealing‘ verstehen: Statt eines kontinuierlichen Zeitplans gibt es diskrete Schichten. Jede Schicht besteht aus einem Schritt mit dem Problem-Hamiltonian (bewertet gute/schlechte Lösungen) und einem Schritt mit einem Mixer-Hamiltonian. Dieser erzeugt eine Exploration in der Energie-Landschaft, ähnlich wie der Driver-Hamiltonian. QAOA Annealing bedeutet das klassische Optimieren von einstellbaren Parametern in Schaltkreisen (Schaltkreis-Winkel).
In beiden Fällen, QAOA und Quantum Annealing, wird das klassische Optimierungsproblem in einen Ising Hamiltonian umgesetzt. Im Falle von QAOA wird dieser als QC-Schaltkreis implementiert, im Falle von Quantum Annealing als Qubit-Netzwerk.



