Kurzfassung: Dieser Beitrag zeigt, wie sich die demokratische Qualität in Ost- und Westdeutschland von 2000 bis 2025 entwickelt und welche Impulse sie stärken oder schwächen. Im Osten wie im Westen ist der Zeitraum um das Jahr 2015 entscheidend für die Entwicklung der demokratischen Qualität. Mit gewissen Unterschieden sinkt sie bis heute für Ost- und West-Deutschland. Der Blog-Beitrag ist explorativ, d.h. er liefert trotz des völlig neuen theoretischen Ansatzes gut nachvollziehbare Ergebnisse: Es wird deutlich, dass zu viel medialer Streit und Polarisierung das Niveau schnell drücken, während anhaltende, sichtbare Zusammenarbeit es hebt. Debatten helfen nur, wenn sie fokussiert bleiben und mit konkreter Umsetzung verbunden sind.
Für die Erstellung dieses Blog-Beitrages habe ich fast ausschließlich ChatGPT 5.0 und in Teilen Version 5.1 benutzt. Es waren keine anderen AI Systeme notwendig: In den letzten Wochen hat sich die Qualität von ChatGPT 5.0 in der Modellierung und der Code-Erzeugung deutlich verbessert. – Mir sind keinerlei Fehler aufgefallen. Die Fähigkeit auch lang zurückliegende Ergebnisse der anderen Blog-Beiträge zu verwenden oder Verknüpfungen zwischen alten und neuen Ergebnissen herzustellen, ist sehr gut gewesen. Für die Qualitätssicherung habe ich die Systeme Claude, DeepSeek und Mistral deshalb nicht mehr verwendet; zumal die Review-Ergebnisse der drei Systeme im Laufe der QSD Blog-Beiträge immer stereotyper wurden. Es wurde krampfhaft versucht wissenschaftliche Kriterien an die Blog-Beiträge anzulegen, u.a. wurde daraufhin gewiesen, dass den Beiträgen eine solide empirische Basis fehle. – Dies ist natürlich korrekt, zeigt aber gleichzeitig, dass den Systemen ein ‚Verständnis‘ für die Intention der Beiträge fehlt. Außerdem wurden zurückliegende Beiträge, aber auch Anhänge und Graphiken nicht oder nur unzureichend berücksichtigt. Nach meiner Einschätzung ist die Kluft zwischen ChatGPT 5.0 und den anderen AI Systemen wieder deutlich größer geworden. Leider trifft die positive Einschätzung von ChatGPT 5.0 für ChatGPT 5.1 nicht zu: Die Qualität in Inhalt, in Modellierung und in Code-Erzeugung war unter Berücksichtigung zurückliegender Arbeitsergebnisse deutlich schlechter! – Das Arbeiten mit der neuen Version, wie so oft in der Vergangenheit, war zeitraubend und anstrengend.
Ziel dieses fünften Teils der Quantum Spiral Dynamics Blog-Reihe ist es, auf der Basis des Ost-West-Deutschland-Modell 2000-2025 eine gesellschaftliche Transformation Deutschlands zu modellieren. – Die Ergebnisse sind ohne Einschränkungen auch auf organisationale Transformationen anwendbar. – Ich komme auf diese Aussage am Ende des Blog-Beitrages wieder zurück.
In [1] verstehen wir unter einer Transformation eine Veränderungsarbeit, für die der Ausgangspunkt der Veränderung zwar bekannt ist, jedoch das Ziel und der Weg zum Ziel unbekannt sind. – Das Ziel wird allenfalls vage erfasst, in dem eine bessere Adaptionsfähigkeit an einen Kontext angestrebt wird. Dies trägt der Tatsache Rechnung, dass man in komplexen Systemen weder das Veränderungs-Ziel noch den Weg zum Ziel strikt vorgeben kann.- Beides kann sich im Laufe der Veränderungsarbeit ändern.
Veränderungsarbeit bezieht sich sowohl auf Individuen als auch auf Organisationen oder Gesellschaften, oder auf alle drei sozialen Ebenen gleichzeitig: Falls eine Organisation oder eine Gesellschaft in ihren kulturellen Strukturen, also im Kulturpotential A(t, s) transformiert werden soll, ist es notwendig, dass einige Individuen schon vorab über die relevanten SD-Werte-Meme verfügen. Soll zum Beispiel das Kulturpotential einer Organisation oder Gesellschaft innovativer und empathischer werden, so ist dieses Unterfangen völlig aussichtlos, falls nicht einige innovative Individuen durch ihre Offenheit, Kreativität und Empathie die Transformation anstoßen und führen.
Abbildung 1 verdeutlicht den Transformationsprozess als iteratives Wechselspiel von Individuen und sozialem Umfeld U:
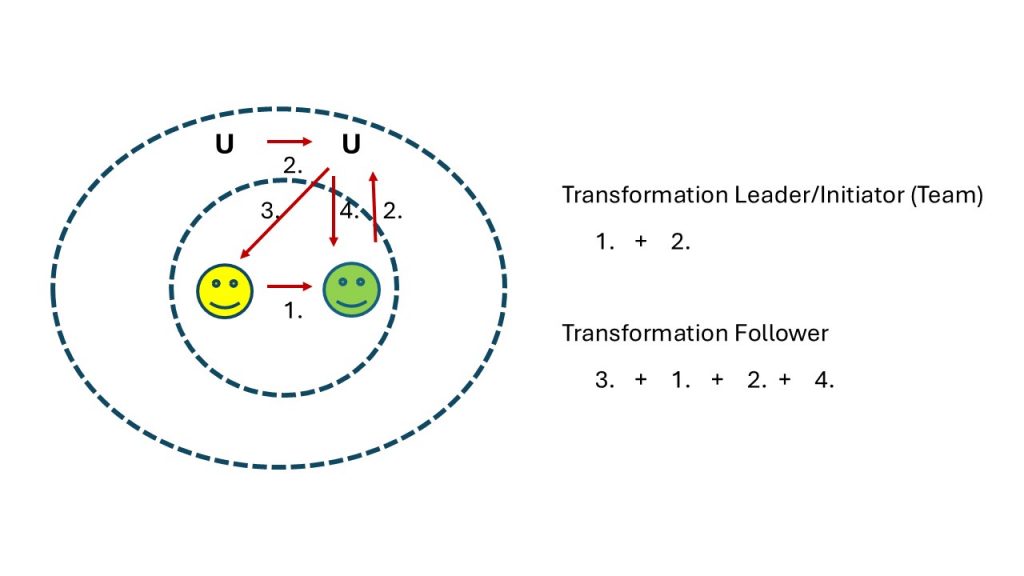
Abbildung 1: Diese Abbildung skizziert die Rückkopplung von individueller Transformation und Kontext-Transformation. Der Kontext wird mit U für Umfeld gekennzeichnet und die Individuen durch Smileys. Ein oder mehrere Individuen agieren im Team als Transformation Leader bzw. Initiator. Es kann notwendig sein, dass sie ihr Mindset für die anstehende organisationale Transformation selbst ändern. – Dies wird durch den Übergang 1. angedeutet. In jedem Fall ist es wichtig, dass das Transformation Team ein gemeinsames Bild, ein Collective Mind, von der Kulturpotential-Transformation entwickelt. Das Umfeld U wird auf dieser Basis einer ersten Transformation, angedeutet durch 2., unterzogen. Das geänderte Umfeld wirkt auf die Transformation Follower und Leader, angezeigt durch 3. und 4., zurück. Diese verändern ihr Verhalten, ggf. sogar ihre Werte und Glaubenssätze, und transformieren ihrerseits das Umfeld wieder, angezeigt durch 2. Das geänderte Umfeld wirkt auf die Individuen zurück, angezeigt durch 4.. Es entsteht iterativ ein selbstkonsistenter Transformationsprozess, der im Idealfall einem Plan-Do-Check-Adapt (PDCA) Prozess folgt [1].
Aus Abbildung 1 kann man sofort erkennen, dass eine Deutschland Transformation, hin zu einem empathischen, sozialen und innovativen, oder gar vernetzt und ganzheitlich handelndem Land, sehr wenig Aussicht auf Erfolg hat: Deutschland fehlen die politischen Führungskräfte, die ein entsprechendes Werteprofil haben bzw. gewillt sind ein solches zu erwerben.
Aber selbst wenn die Transformation Leader über das entsprechende Bewusstsein und die nötigen Fähigkeiten der Umsetzung verfügen, ist eine Transformation ein sehr schwieriges, wenn nicht sogar aussichtloses Unterfangen. – Denn es geht immer darum, kulturelle Strukturen im Umfeld zu verändern.
Der Blog-Beitrag verdeutlicht diese Aussage mittels des QSD-Modells: Als Ausgangsbasis benutze ich das aus empirischen Deutschland-Daten abgeleitete Kulturpotential der vorhergehenden Blog-Beiträge. – Ich nenne es das ursprüngliche Potential. Mit Hilfe dieses Kulturpotentials berechne ich zwei weitere (verfeinerte) Kulturpotentiale:
- A_coup (coup steht für coupled) bezeichnet ein dynamisches effektives Kulturpotential, das aus einer gewöhnlichen Differentialgleichung (ODE) erzeugt wird. Diese ODE lehnt sich an Differentialgleichungen zum Feldtensor der Quantenfeldtheorie an: Das ursprüngliche Kulturpotential wirkt in dieser ODE als ‚Treiber‘. Zusätzlich werden die Pfadinformationen der Agenten aus einer Schrödingergleichung mit effektivem Kulturpotential ‚eingespeist‘. – Wie ich in den vorherigen Blog-Beiträgen gezeigt habe, sind die Pfadinformationen die individuellen Wert-Transformationen der drei Agentenpopulationen Blau, Orange und Grün.
Es entwickelt sich ein selbstkonsistentes effektives Kulturpotential, entsprechend dem Selbstkonsistenz-Prozess aus Abbildung 1: Die Agenten beeinflussen das Potential, also das Umfeld, und das Potential koppelt wieder auf die Agenten zurück. A_coup wird jeweils für Ost- und West-Deutschland berechnet. Das ursprüngliche Potential, auch wenn es von Ort und Zeit abhängt, ist kein selbstkonsistentes Potential, das aus einer Dynamik ermittelt wurde. – Es spiegelt ein von Individuen wahrgenommenes Potential an Hand von nachgefragten Kriterien wieder. In diesem Sinne kann es sinnvoll sein, die (potentiellen) Auswirkungen einer Selbstkonsistenz zu überprüfen, was ich mit A_coup tue! – Ich verweise für die verwendeten Formeln auf den Anhang 1 ‚QSD Formeln‘. - A_mix (mix steht für mixed) basiert auf A_coup und berechnet eine Potentialmischung jeweils für Ost- und für West-Deutschland. Ost-Deutschland wird 30% des West-Deutschland Potentials beigemischt und umgekehrt. Damit modelliere ich einen Kulturaustausch zwischen Ost und West, also einen möglichen Lerneffekt von West nach Ost und umgekehrt.
Um die gesellschaftliche Transformation von Ost- und West-Deutschland einzuschätzen, benötige ich ein Kriterium, mit dem ich den Zustand von Ost- und West-Deutschland vor und nach der Transformation ‚beurteile‘.
Ich führe hierfür einen statischen Demokratieindex ein. Dieser Demokratieindex wird nur aus Größen bisheriger QSD-Berechnungen ermittelt. Ich definiere den statischen Demokratieindex,
- der mit Kohärenz, Kohäsion und Werte-Vielfalt steigt,
- und der mit der sozialen Spannung, ermittelt aus dem Feldtensor, sinkt.
Für die damit verbundene mathematische Form verweise ich auf Anhang 1 ‚QSD Formeln‘. Zusätzlich zum statischen Demokratieindex definiere ich eine einfache ODE, in die der statische Demokratieindex als ‚Treiber‘ eingeht. – Ich erhalte einen (einfachen) dynamischen Demokratieindex. Für die dazugehörige Formel verweise ich ebenfalls auf den Anhang 1.
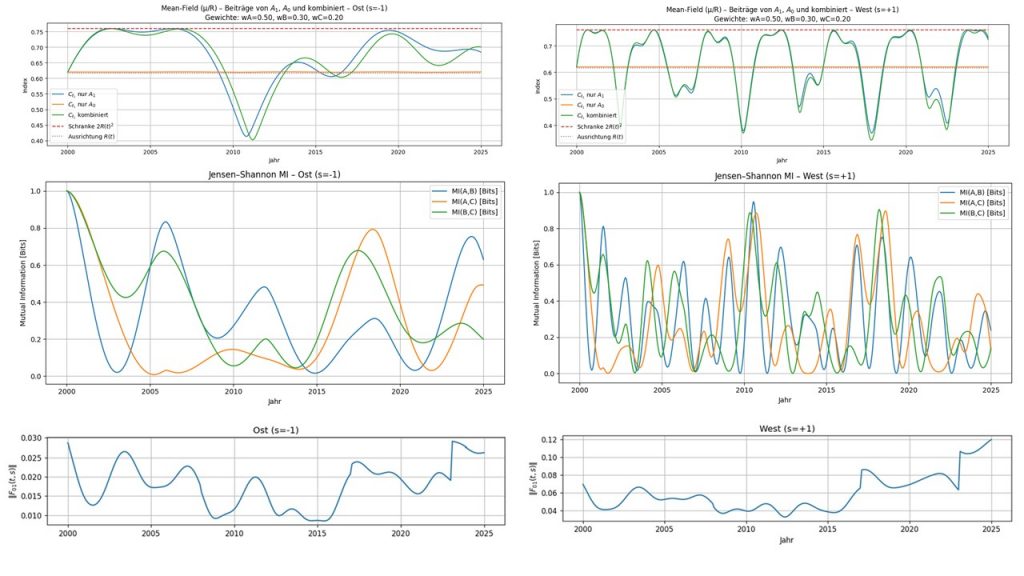
Abbildung 2 zeigt den statischen und dynamischen Demokratieindex für Ost-Deutschland (linke Seite) und West-Deutschland (rechte Seite). Der dynamische Demokratieindex läuft in allen Fällen dem statischen etwa 1-2 Jahre nach.
Da Kohärenz, Kohäsion und Spannung in den Demokratieindex eingehen, zeigt Ost-Deutschland bis ca. 2020/22 eine fast gleichbleibend hohe Demokratie, wohingegen im Westen, wie bei der Kohärenz (man siehe den vorherigen Blog-Beitrag), tiefe Einschnitte zu sehen sind. Die Erzeugung des selbstkonsistenten Potentials A_coup erzeugt in West-Deutschland keine auffallenden qualitativen Veränderungen. In Ost-Deutschland erzeugt die Selbstkonsistenz einen ‚Verfall‘ der Demokratie um 2015: Damit nähern sich Ost- und West-Deutschland ab 2015 sehr stark aneinander an.
Die Mischung A_mix sorgt im Osten ab ca. 2015 für einen geringeren Zuwachs des Demokratieindex als im Westen: Der Westen profitiert also mehr vom Osten als umgekehrt. – Unter dem Vorbehalt, dass wir hier eine sehr spekulative Theorie entwickelt haben, sind dies schon sehr erstaunliche Aussagen!
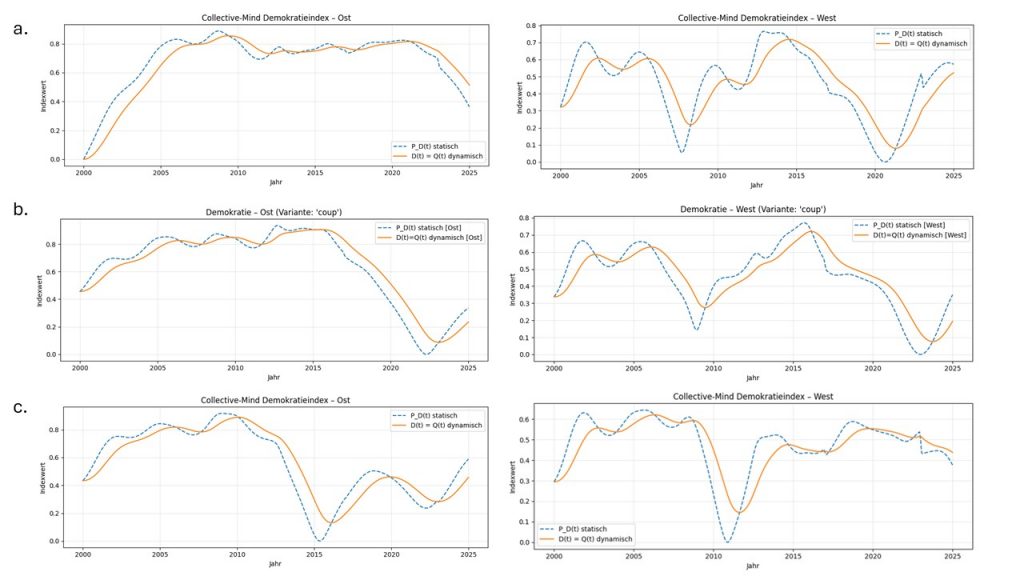
Abbildung 2: Die Zeile a. enthält den Demokratieindex Ost- und West-Deutschlands für das aus empirischen Daten gewonnene ursprüngliche Kulturpotential. Zeile b. zeigt das selbstkonsistente Kulturpotential A_coup berechnet aus einer Differentialgleichung für A(t, s). In A_coup geht das aus empirischen Daten gewonnene Kulturpotential als ‚Treiber‘ ein und die Pfade der drei Agentenpopulationen (Blau, Orange und Grün) wirken als Rückkopplung. Man siehe hierzu den Anhang 1 ‚QSD Formeln‘ mit folgenden Parametern: gamma = 0.3, g = 1.0, beta = 3.0, alpha_0 = 0.2 und alpha_1 =0.35, kappa = 1.0.
Die Zeile c. zeigt A_mix, mit eta = 0.3 als Mischungsfaktor: In A_coup für Ost- und West-Deutschland werden jeweils 30% des jeweils anderen Kulturpotentials ‚beigemischt‘. Diese Mischung modelliert ein gewisse Annäherung von Ost- und West-Deutschland.
Abbildung 3 zeigt, mit A_mix als Ausgangs-Potential, die Ergebnisse einer ‚wenig gelungenen‘ Transformation. Wir nehmen an, dass ein Politiker-Team (d.i. das Transformation Leader Team) drei Werte-Impulse von bis zu jeweils 10 Jahren für jeweils Ost- und West-Deutschland gestaltet. Ich habe der Übersicht wegen nur drei Impulse ausgewählt. – Auch in der Praxis dürfte es sehr schwer sein, mehr als drei Impulse nachhaltig zu führen.
Die drei Werte-Impulse entsprechen drei Parameterfunktionen von drei Generatoren. Es sind λ1, λ2 und λ7 (man siehe den Anhang 3 ‚Übersicht der Generatoren und ihrer QSD Interpretation‘ des vorherigen Blog-Beitrages):
λ1 realisiert einen institutionellen Austausch von Blau und Orange, also zwischen Pflicht- und Sicherheits-Strukturen sowie Erfolgs- und Wettbewerbs-Strukturen
λ2 realisiert einen narrativen Austausch (Diskurs, Polarisierung) von Blau und Orange, also zwischen Pflicht- und Sicherheits-Narrativen sowie Erfolgs- und Wettbewerbs-Narrativen
λ7 realisiert einen narrativ-medialen Austausch von Orange und Grün, also zwischen Erfolgs- und Wettbewerbs-Narrativen sowie sozialen Empathie- und Sinn-Narrativen
Ich skizziere ein Transformations-Szenario, in dem für λ1 und λ2 positive Impulse verwendet werden und für λ7 ein negativer Impuls angenommen wird.
Für Ost-Deutschland:
λ1: Integrations-/Aufbauimpulse 2003–2008 und um 2010
λ2: Diskursimpuls um 2012 (mediale Legitimationsdebatten)
λ7: starker negativer Konfliktimpuls ab 2015 und um 2021
Für West-Deutschland:
λ1: längerer pro-EU/Globalisierungsimpuls 2004–2015
λ2: Diskursimpuls 2015–2021 (Migration/Identität)
λ7: später Konfliktimpuls 2018–2024 (Corona/Öko/Klima-Konflikte)
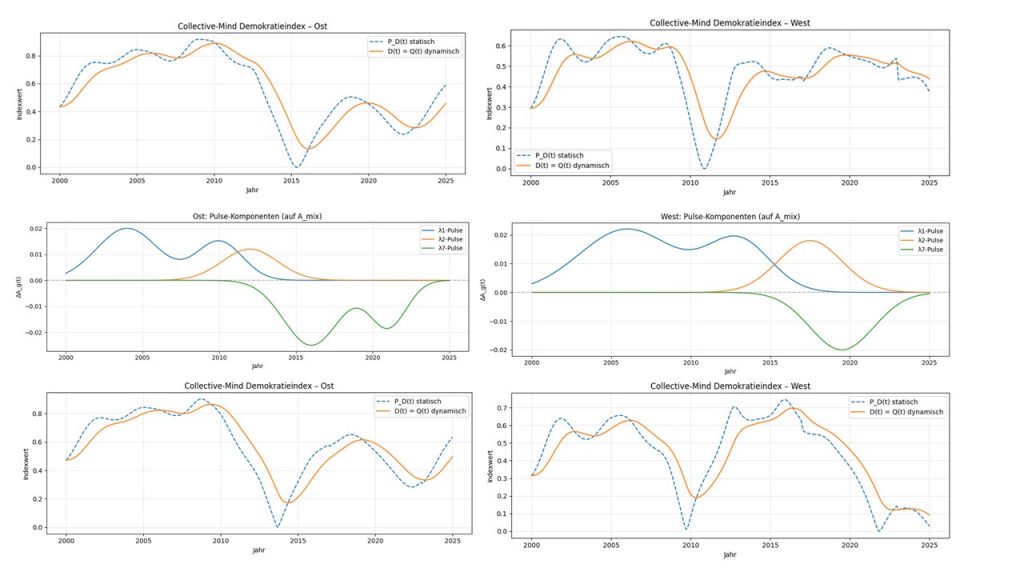
Abbildung 3: Die erste Zeile der Abbildung zeigt A_mix für Ost- und West-Deutschland als ‚Start‘ der dargestellten Transformation. Auf A_mix werden Werte-Transformations-Impulse angewendet. Diese Werte-Transformations-Impulse sind in der nächsten Zeile zu sehen. Man beachte, dass die Impulse nur etwa 2.5% des ursprünglichen Kulturpotentials ausmachen. Alle Impulse sind für Ost- und West-Deutschland unterschiedlich. Die dritte Zeile zeigt die resultierenden Konsequenzen für den Demokratieindex. Die Impulse für Ost- und West-Deutschland sind nicht gleich, trotzdem kann man feststellen, dass Ost-Deutschland die Impulse besser ‚verkraftet‘. Obwohl die Lambda 1 und 2 Impulse in Ost- wie West-Deutschland positiv sind, die Politik also einen ‚guten Job macht‘ sorgt der negative Lambda 7 Impuls in beiden Teilen Deutschlands für einen starken Einbruch im Demokratieindex: In Ost-Deutschland ist es vor allem der ungeeignete Umgang mit Migration und Corona. In West-Deutschland ist es vor allem der ungeeignete Umgang mit Corona und Öko/Klimakrise. In West-Deutschland fällt der Demokratieindex nach 2020 ins ‚Bodenlose‘.
Im Folgenden verdeutliche ich, wie eine bessere Transformation aussehen kann: Abbildung 4 zeigt eine Transformation, für die alle Impulse der drei Potentialkomponenten (dies sind die angegebenen Generatoren λ1, λ2, λ7) explizit demokratie-stärkend sind. Die Impulse setzen folgende Schwerpunkte:
Ost:
- 2002–2008: Aufbau demokratischer Institutionen (λ1)
- 2012–2022: Diskurs- und Versöhnungsimpulse zu Sicherheit und Markt (λ2)
- 2015–2025: erneute integrative Demokratie-Impulse (λ7)
West:
- 2003–2010: EU-/Rechtsstaats-/Modernisierungspulse (λ1)
- 2014–2020: pluralistischer Diskurs rund um Migration/Klima (λ2)
- 2020–2025: inklusiver Identitätsimpuls gegen Polarisierung (λ7)
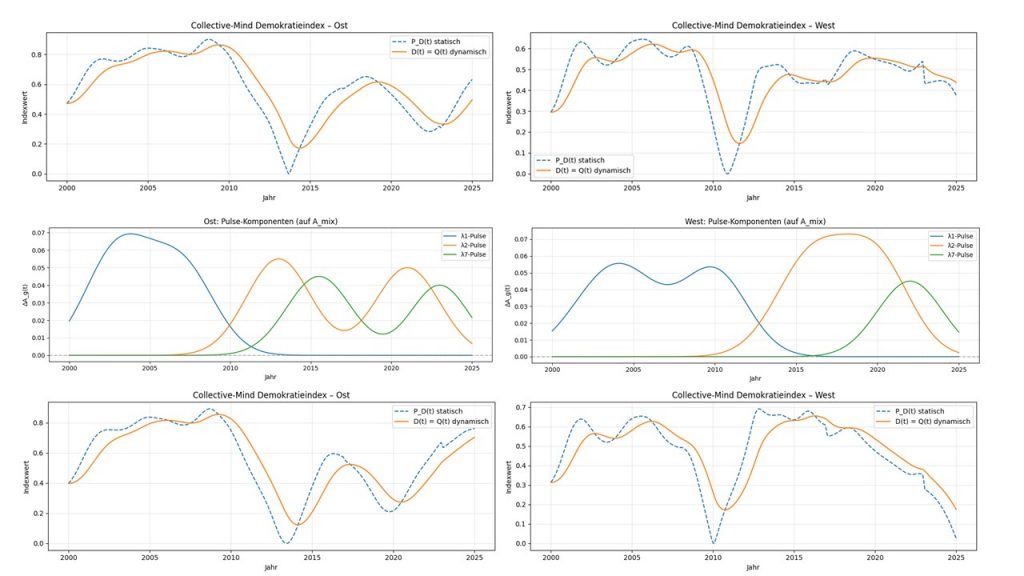
Abbildung 4: Die erste Zeile der Abbildung zeigt A_mix für Ost- und West-Deutschland. Auf A_mix werden Werte-Transformations-Impulse angewendet. Diese Werte-Transformations-Impulse sind in der nächsten Zeile zu sehen. Man beachte, dass die Impulse etwa 10% des ursprünglichen Kulturpotentials ausmachen. Hier ist im Gegensatz zu Abbildung 3 der Impuls für Lambda_7 positiv. Beides ist beabsichtigt, um zu zeigen, wieviel ‚Energie‘ notwendig ist, um eine merkliche Veränderung herbeizuführen. Die Impulse für Ost- und West-Deutschland sind unterschiedlich, denn sie sollen den jeweiligen gesellschaftlichen Transformations-Anforderungen gerecht werden: Die Auswahl der Impulse erfolgte für den Blog-Beitrag nicht systematisch: Es könnten andere Impuls-Kombination wesentlich erfolgreicher sein. Das Auffinden dieser dürfte sehr aufwendig sein: Es war lediglich mein Ziel, die grundlegende Idee der Werte-Transformations-Impulse zu demonstrieren. Die dritte Zeile zeigt die resultierenden Konsequenzen für den Demokratieindex: Sowohl für Ost-Deutschland als auch für West-Deutschland haben die Impulse jetzt eine deutlich stärkende Wirkung der demokratischen Qualität: Für West-Deutschland kann man erkennen, dass der starke Lambda 7 Impuls den Demokratieindex zwischen 2015-2020 hebt, jedoch der Effekt verschwindet sobald Lambda 7 zurückgeht.
Die Ergebnisse der Abbildung 3 und 4 stehen unter dem Vorbehalt, dass ich für die Berechnung der Auswirkungen der Werte-Transformations-Impulse keine selbstkonsistente Berechnung wie für A_coup vorgenommen habe. Aufgrund der kleinen Amplituden der Werte-Transformations-Impulse erwarte ich keine merklichen Änderungen.
Abbildung 5 zeigt die Differenz des Demokratieindex für Ost- zu West-Deutschland auf der Basis der Berechnungen für Abbildung 4. Entgegen meinen Erwartungen zeigt Ost-Deutschland teilweise einen deutlich höheren Demokratieindex als West-Deutschland.- Und selbst im Mittel ist der Demokratieindex für Ost-Deutschland über den Zeitraum 2000-2025 noch (etwas) höher als in West-Deutschland. Diese Aussage gilt für alle o.g. Kulturpotentiale!
Man könnte dies als Artefakt einer spekulativen Theorien abtun, wären da nicht die vielen Übereinstimmungen mit den realen politischen Situationen. – Ich gehe davon aus, dass die Differenz des Demokratieindex wahrscheinlich die Realität widerspiegelt, also stelle ich statt dessen meine eigenen Vorurteile in Frage.
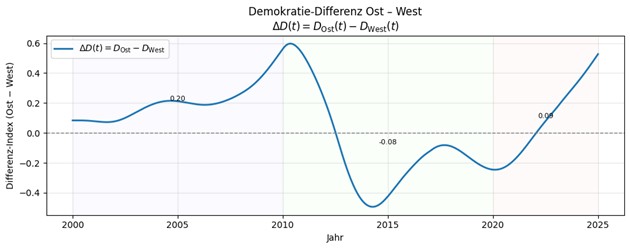
Abbildung 5: Diese Abbildung zeigt den Unterschied im Demokratie-Index von Ost und West, auf der Basis der Berechnungen zu Abbildung 4. Die in der Abbildung enthaltenen Zahlen zeigen den jeweils gemittelten Demokratie-Unterschied für verschiedene Zeiträume: 0.20 für den Zeitraum 2000-2010, -0.09 für den Zeitraum 2010-2020 und 0.09 für den Zeitraum 2020-2025. Dies bedeutet, dass in diesem Fall bis 2010 der Demokratieindex für Ost-Deutschland deutlich höher war als für West-Deutschland und im Zeitraum danach sich im Mittel keine Unterschiede zeigen.
Die Ergebnisse des Blog-Beitrages weisen erstaunliche Parallelitäten zur Realität auf. – Die Tendenzen im hier ermittelten Demokratieindex decken sich meines Erachtens mit dem Hauptergebnis der Mitte-Studie 2025 [2, 3]: „Nur noch 52 Prozent der Befragten finden, dass die Demokratie im Großen und Ganzen ganz gut funktioniert. Ein Viertel verneint dies – das ist ein Höchstwert seit 2016….Die Zahl derer, die sich klar demokratisch positionieren, nimmt ab. Immer weniger lehnen konsequent alle wirklich harten extrem rechten Aussagen ab, anhand derer wir die Einstellung erfassen.“
Der Beitrag zeigt, wie sich die demokratische Qualität in Ost- und Westdeutschland von 2000 bis 2025 entwickelt und welche Impulse sie stärken oder schwächen. Im Osten steigt sie bis etwa 2010/12 deutlich, bricht 2014–2016 ein und erholt sich danach nur teilweise.
Im Westen hält sie bis 2014 gut durch, fällt dann extrem stark ab, kann sich zwar wieder bis 2020 erholen, fällt danach aber stetig bis 2025. Deutlich wird: Zu viel Streit und Polarisierung drücken das Niveau schnell, während anhaltende, sichtbare Zusammenarbeit es hebt. Debatten helfen nur, wenn sie fokussiert bleiben und mit konkreter Umsetzung verbunden sind – endloses Reden ohne Ergebnisse schadet. Im Osten wirken zuerst De-Eskalation und klug gestaltete Beteiligung; darauf könnten! Integrations- und Aufbauprojekte erfolgreich aufbauen. Im Westen braucht es vor allem spürbare Verbesserungen im Alltag und in der Verwaltung, bevor große Debatten tragfähig werden könnten! Der Blog-Beitrag ist explorativ, er liefert keine endgültigen Wahrheiten, sondern gut nachvollziehbare Handlungs-Orientierungen. Die Kernbotschaft ist: Weniger Polarisierung, mehr fokussierter Diskurs und früh sichtbare gemeinsame Erfolge stärken die demokratische Qualität.
Die Anwendbarkeit auf die Transformation von Organisationen ergibt sich meines Erachtens ohne Einschränkungen: Natürlich ist es notwendig, ein Ausgangs-Kulturpotential zu erstellen. Dies erfordert die empirische Erhebung von Daten, ähnlich wie ich sie für die vorliegende Analyse benutzt habe. Mit Hilfe dieser Daten ist es dann möglich, alle gezeigten Berechnungen durchzuführen. Der Demokratieindex kann auch in Organisationen verwendet werden, ggf. ergänzt um weitere Faktoren, wie den Faktor für die Ziel-Orientierung. In einem PDCA-ähnlichen Prozess formulieren Führungskräfte Annahmen über sinnvolle Impulse und geben diese in die hier vorgestellte theoretische Impuls-Analyse ein. Diese Impuls-Analyse dient einer ersten theoretischen Validierung bezüglich der Wirkung der Impulse. Falls diese Validierung befriedigende Ergebnisse zeigt, werden die Impulse mit passenden Maßnahmen in der Praxis umgesetzt. Erkenntnisse aus der Praxis fließen in die Theorie ein und der so begonnene PDCA Zyklus wird mit weiteren Iterationen fortgesetzt.
Die theoretische Basis lässt sich natürlich weiter verbessern, in dem alle acht Generatoren für die Impuls-Gestaltung verwendet werden. Der Aufwand für die Berechnungen steigt, aber dies dürfte nicht wesentlich sein. Viel aufwendiger ist die Analyse von Ursache und Wirkung der Impulse. Um solche Zusammenhänge zu ermitteln sind umfangreiche Variationen in der Impulszusammensetzung nötig.
Eine massive Erweiterung der Kulturdynamik stellt der Übergang von der SU(3) zur SU(8) dar, also der Berücksichtigung aller 8 Spiral Dynamics Bewusstseinsebenen. Um autokratische Persönlichkeiten und ihren Einfluss auf die Demokratie zu modellieren, sind die Bewusstseinsebenen beige, violett und rot notwendig. Falls demokratische Persönlichkeiten als Gegengewichte auftreten, kommen die Ebenen gelb und türkis hinzu. – Für eine erste grobe Einordnung der Bewusstseinsebnen, verweise ich auf den ersten Blog-Beitrag zur QSD Blog-Reihe vom August 2025.
Diese Erweiterung übersteigt bei weitem mein Ziel, die Machbarkeit des QSD-Ansatz aufzuzeigen.
Ich werde im nächsten und voraussichtlich letzten QSD Blog-Beitrag versuchen, eine Demokratie-Analyse für die Länder USA, Ungarn, Ukraine und Deutschland durchführen, um zu sehen, ob es Parallelitäten zu der Blog-Reihe ‚Von der gesellschaftlichen Kernschmelze…‘ vom April 2025 bis Juni 2025 gibt.
[1] Oswald A et al. (2017) Project Management at the Edge of Chaos, Springer
[2] ZDF (2025) Mitte-Studie 2025, https://www.zdfheute.de/politik/deutschland/mitte-studie-demokratie-rechtsextremismus-100.html
[3] Friedrich Ebert Stiftung (2025) Mitte-Studie 2025, https://www.fes.de/mitte-studie
Anhang 1
QSD-Formeln
Selbstkonsistentes Kulturpotential A_coup
![]()
![]()
![]()
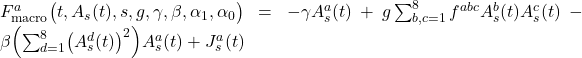
![]()
![]()
![]()
![]()
Ost-, West- Mischfeld A_mix
für Ost
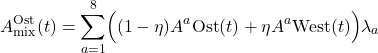
für West
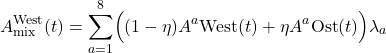
Kohärenz–Kohäsion-Index
Misst die „gerichtete kollektive Stärke“ eines sozialen Feldes, also den Collective Mind, als Produkt aus Kohärenz und Kohäsion.
![]()
Vielfalt (normierte Entropie)
Wahrscheinlichkeiten je Agent (über Komponenten )
![]()
Gemittelte Verteilung über die drei Agenten
![]()
Entropie der gemittelten Verteilung (zeitabhängig)
Normierte Vielfalt
![]()
Spannung (normierte Feldstärke)
Misst die soziale Belastung bzw. Systemspannung über den Feldstärkentensor.
![]()
Normierter Kohärenz–Kohäsion-Index
Skaliert auf den Bereich , damit es mit anderen Größen vergleichbar wird.
![]()
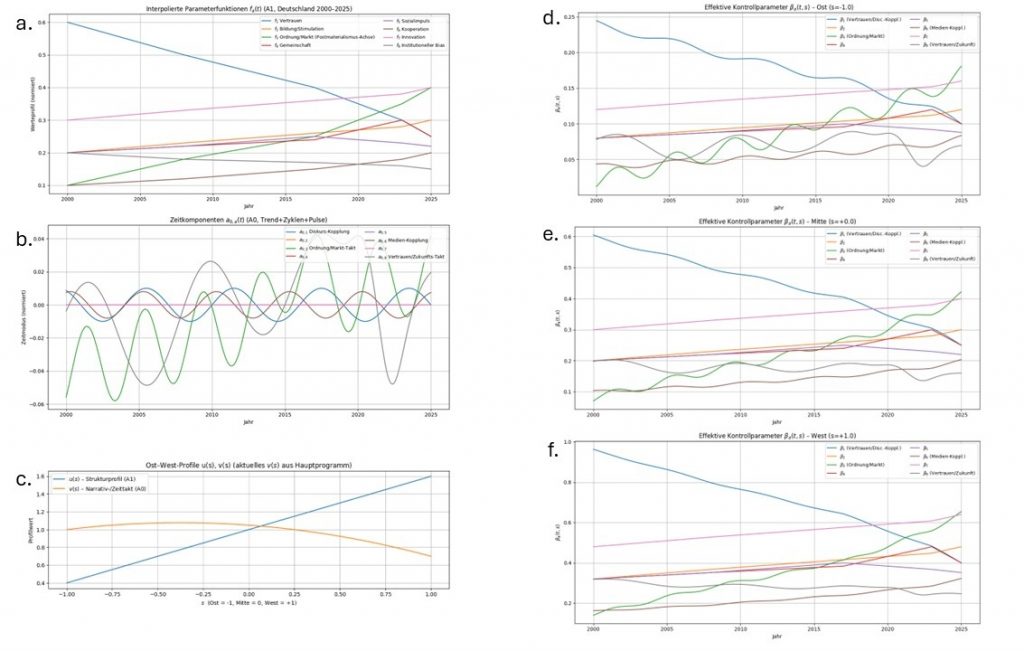
Statischer Demokratie-Index
Misst den „momentanen“ Demokratiezustand ohne Trägheit:
mehr Kohärenz/Kohäsion + mehr Vielfalt – Spannung.
![]()
Dynamischer Demokratie-Index
Modelliert den kollektiven Demokratie-„Mindset“-Pfad als träges Gedächtnissystem.
Dynamische Gleichung
![]()
Startbedingung
![]()
Definition des dynamischen Demokratieindex
![]()
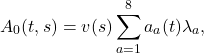
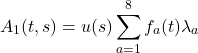
![Rendered by QuickLaTeX.com \begin{equation*}||F_{\mathrm{eff}}(t,s)||= \frac{||F_{01}(t,s)||}{\displaystyle \max_{t'\in[t_0,t_1]} ||F_{01}(t',s)|| + \varepsilon},\qquad \varepsilon>0\ \text{klein.}\end{equation*}](https://agilemanagement40.com/wp-content/ql-cache/quicklatex.com-d2526855e40d98a95bdc545e9d486c11_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*}C_{\ell_1}(t,s)=R(t,s)^2 \left[\left(\sum_{i=1}^{3}\lvert\hat{\mu}_i(t,s)\rvert\right)^{2}-1\right]\le 2 R(t,s)^2\end{equation*}](https://agilemanagement40.com/wp-content/ql-cache/quicklatex.com-5fb31f3e5d721b60d706a14a8907d2f4_l3.png)