Eine Warnung vorweg: Ich benutzte im Blog Mathematik und AI Techniken, da ich versuche, den Begriff Collective Mind damit besser auszuleuchten. Vielleicht motiviert dies den ein oder anderen Leser, den Blog-Beitrag genau aus diesem Grunde zu lesen.
Der Begriff Collective Mind wurde erstmals 2007 von Jens Köhler und mir, im Zusammenhang mit der Erstellung unseres Buches „Die Collective Mind Methode“, geprägt [1]. Später ist der Collective Mind, als einer der zentralen Begriffe, in Management 4.0 eingegangen.
Wir verstehen unter Collective Mind (CM) einerseits einen kollektiven Flow-Zustand, der für Team oder organisationale Hochleistung steht und andererseits steht er auch für einen Operator, also Modelle und Theorien, der diesen Zustand beschreibt und herbeiführt.
Wir benutzen in der Collective Mind Theorie zwar verschiedene Modelle (Persönlichkeitkeitsmodelle, Wertemodelle, Team-Heterogenitätsmodelle, Kommunikationsmodelle usw.) mit denen wir den Collective Mind herbeiführen; und das funktioniert sehr gut, wie wir in mehr als 15 Jahren Praxis zeigen konnten, jedoch ist es uns bisher nicht gelungen den Flow-Zustand selbst, den Collective Mind, durch ein Modell oder eine Theorie zu beschreiben. Wir arbeiten stattdessen mit Metaphern oder wir verwenden Stellvertretermodelle, kurz Proxies, um ihn zu beschreiben. Diese Proxies sind:
- Mitwirkungs- und Redezeit: Der CM ist dann besonders stark, wenn alle Teammitglieder nahezu gleichstark mitwirken, also sie zum Beispiel in nahezu allen Teammeetings anwesend sind und ihre Redezeit nahezu gleich verteilt ist.
- Ähnlichkeit in der Wort- und Bild-Wahl: Der CM ist dann besonders stark, wenn alle Teammitglieder ähnliche Worte und/oder Bilder benutzen, um einen Projektsachverhalt zu beschreiben. – Es findet ein Spiegeln im gesprochenen Wort und im Bild statt.
- Zufriedenheit: Der CM ist besonders stark, wenn alle Teammitglieder der Arbeit im Team eine sehr hohe Zufriedenheit attestieren und sie das Gefühl haben einen sinnvollen Beitrag zu leisten.
- Spiegeln der Körpersprache: Der CM ist besonders stark, wenn alle Teammitglieder in ihrer Körpersprache die Köpersprache der anderen spiegeln.
Im Idealfall treffen für ein CM Hochleistungsteam alle diese Proxies gleichzeitig zu.
Diese Stellvertretermodelle können sich auch über die Zeit entwickeln: Zum Beispiel benutzen die Teammitglieder am Anfang völlig unterschiedliche Beschreibungen (Sätze, Bilder), um ein Projektziel oder einzelne Anforderungen zu konkretisieren. Steigt der Collective Mind, werden die Unterschiede geringer. Jedoch kann im Team etwas passieren, das den Collective Mind zerstört oder wieder ins Wanken bringt. Die Unterschiede in den Proxies werden entsprechend wieder größer. Beispiele für solche Ereignisse, die den CM wieder verändern, sind neue Teammitglieder oder wechselhafte Anwesenheiten von Teammitgliedern oder neue Erkenntnisse, die nicht von allen im gleichen Maße gesehen und geteilt werden.
Die Leser dieses Blogs dürften diese empirischen Aussagen bei geneigter Bobachtung in ihren Teams sehr schnell bestätigen. Ich verweise diesbezüglich auch auf das Whitepaper von Armatowski et. al., das anlässlich der IPMA Research Conference zum Thema Selbstorganisation erstellt wurde [2]. – Das Whitepaper skizziert für das Autorenteam den Prozess der Selbstorganisation, also der Ausbildung eines CM’s, während der IPMA Research Hackdays 2020.
Im Bereich der Wissenschaften, insbesondere derjenigen, die Sachverhalte auch mathematisch beschreiben, hat man sich inzwischen weitgehend daran gewöhnt die Realität mit den Proxies für die Realität gleichzusetzen: Zum Beispiel werden elektrische Erscheinungen einem elektrischen Feld E zugeschrieben (Fett gedruckte Buchstaben bezeichnen hier eine sogenannte Vektorgröße, die durch einen Betrag und eine Richtung beschrieben wird). – Wahrscheinlich käme kaum jemand auf die Idee, E als Proxy zu betrachten. – Falls es doch mal durch einen genialen Wissenschaftler geschieht, bringt dieser die Erkenntnis einen Schritt weiter, in dem er die dem Proxy hinterlegten Annahmen radikal hinterfragt.
Alle anderen dürften über Jahrzehnte oder sogar Jahrhunderte hinweg das elektrische Feld E mit der „wahren“ elektrischen Realität gleichsetzen. – Lediglich im Bereich der Quantenmechanik ist diese breite Sicherheit nie so wirklich wahrgeworden. – Die Unterschiede zwischen alltäglicher Erfahrung und quantenmechanischer Beobachtung und den assoziierten Proxies ist nach wie vor zu groß.
Proxies sind also nur Stellvertreter, also Modelle oder Theorien, die unsere Beobachtungen zusammenfassen bzw. abstrahieren. So gesehen ist es sicherlich legitim die obigen Collective Mind Proxies für den „wahren“ Collective Mind zu verwenden. Verwendet man zusätzlich die Mathematik zur Beschreibung, so ergibt sich ein deutlich besseres und erweitertes Verständnis der Zusammenhängen, nicht selten werden Zusammenhänge erst sichtbar. – Eine Aussage, die nach meiner Erfahrung immer gültig ist, vorausgesetzt man berücksichtigt wie auch bei anderen (mentalen) Modellen, dass Proxies nicht zwangsläufig die Realität sind.
Setzt man die mathematische Beschreibung in Technologie, in unserem Fall in Artificial Intelligence Technologie, um, so lässt sich der CM viel besser fassen. Wie wir gleich sehen werden, lassen sich die Collective Mind Proxies in der Praxis gut operationalisieren und gut überprüfen.
Wir führen das mathematische Gebilde „Tensorfeld Collective Mind CM(x,t)“ ein, das vom Ort x und der Zeit t abhängt.
Was verstehe ich darunter?
Im Kontext von Management oder Projekt Management kann man sich sehr gut vergegenwärtigen, dass der Collective Mind wie ein abgeschossener Pfeil eine Richtung haben muss, denn Projektziele oder die Ziele einzelner Personen oder Organisationen werden u.a. durch eine Richtung beschrieben. Er hat auch einen Betrag, nämlich die Energie, die im Team, in der Person oder der Organisation zu diesem Ziel vorhanden ist. Dass der CM sich zeitlich ändern kann, habe ich schon oben erläutert. – Er kann natürlich auch vom Ort abhängen. – Der Collective Mind innerhalb eines (größeren) Teams oder einer Organisation kann durchaus von Ort zu Ort unterschiedlich sein: Verschiedene Sub-Teams eines Teams haben unterschiedliche Collective Minds, verschiedene Sub-Organisationen (Abteilungen) einer Organisation haben wahrscheinlich auch unterschiedliche Collective Minds.
Mit diesen Annahmen setze ich die obigen verbalen Proxies in Mathematik um: Die Aussage „in etwa gleiche Mitwirkungs- und Redezeit“ kann man in Differenzen umsetzen, indem wir die Redezeiten jeder Person mit jeder anderen Person vergleichen. Es entsteht eine Matrix, oder allgemeiner ein Tensor oder Tensorfeld. – Die bekannteste google AI/ML Plattform auf der Basis neuronaler Netzwerk heißt tensorflow, weil Tensoren durch das Netzwerk aus künstlichen Neuronen fließen [3].
Auch die Ähnlichkeit in der Wortwahl kann man durch Differenzen darstellen. Die Differenzen in der Wortwahl bilden ebenfalls ein Orts- und Zeit-abhängiges Tensorfeld.
Auf der Basis der obigen verbalen Proxies führen wir eine mathematische Form für den Operator des Collective Minds, CMO(x,t) (das hochgestellte O steht für Operator), ein:
CMO(x, t) ~ proxyCMO(x, t) = SO(x, t)*MO(x,t)
Diese Gleichung drückt aus, dass wir annehmen, dass das „unbekannte Wesen“ CMO(x, t) näherungsweise durch einen proxyCMO(x,t) beschrieben werden kann; und dass zwei Faktoren – nach jetziger Erkenntnis – diesen proxyCMO(x,t) bestimmen. Ich habe Faktoren gewählt, um auszudrücken, dass im Idealfall alle zwei Faktoren, SO und MO, vorhanden und groß sein müssen, um einen großen CMO(x,t) zu erhalten.
SO(x,t) = Similarity: Dieser Faktor “misst” Mitwirkungs- und Redezeit sowie Wortähnlichkeit (Ähnlichkeiten in Bildern berücksichtigen wir der Einfachheit wegen hier nicht). Wir können diese beiden Proxies gut in einer Größe zusammenfassen: Wählen wir SO(x,t) geeignet, so kann SO(x,t) nur dann eine hohe Similiarity ausweisen, wenn man gleich große Text – oder Redeblöcke miteinander vergleicht und dies kann nur dann der Fall sein, wenn die Teammitglieder in etwa gleich lange anwesend sind und gleichlange sprechen.
MO(x,t) = Mood: Dieser Faktor misst die Stimmung, die Zufriedenheit im Team oder in der Organisation. Dieser Faktor schließt auch die Häufigkeit und Intensität des körperlichen Spiegelns ein.
Ob man mehrere Faktoren benötigt, ist mir zurzeit noch nicht klar, denn SO kann nur dann hoch sein, wenn MO hoch ist. – Nur zufriedene Teammitglieder reden in etwa gleich viel mit einer ähnlichen (spiegelnden) Kommunikation in Sprache und Körper. – Jedoch könnte man Unterschiede zwischen Körpersprache und gesprochenem Wort benutzen, um Dysfunktionalitäten aufzudecken. Hierzu wäre eine entsprechende visuelle AI notwendig und dies geht in jedem Fall weit über diesen Blog hinaus.
Ich tue jetzt mal so, als wenn einige Jahrzehnte verstrichen seien und wir uns wie beim elektrischen Feld E daran gewöhnt hätten, Proxy und Realität gleichzusetzen: Wir setzen also in der obigen Gleichung CMO und proxyCMO gleich und wir nehmen der Einfachheit wegen an, dass die Similarity genügt, um den CMO zu beschreiben:
CMO(x, t) = SO(x, t)
SO(x, t) ist eine symmetrische Matrix deren Elemente Sij(x,t) Differenzen von zwei Vektoren sind, nämlich die Differenz zwischen dem Wortanteil und der Wortwahl des Teammitgliedes i und derjenigen des Teammitgliedes j. Wortanteil und Wortwahl jedes Teammitgliedes werden durch einen Vektor in einem verbalen Raum ausgedrückt.
Jetzt müssen wir „nur noch“ einen geeigneten Operator SO(x,t) finden, der in einem verbalen Raum Vektoren aufspannt. – Ohne die Fortschritte in AI/ML wäre hier das Ende meiner Ausführungen erreicht. – Die enormen Fortschritte in der Verarbeitung der natürlichen Sprache mittels AI/ML, also dem AI/ML-Teilgebiet NLP (Natural Language Processing), machen es mir möglich, weiterzukommen.
Im Jahre 2013 wurde die fundamentale Idee veröffentlicht, Text bzw. Worte in Vektoren zu transferieren: Es werden Worte in einen Vektorraum eingebettet. Deshalb nennt man diese Technik auch word embedding. Word embedding wird auch mit dem Namen der wahrscheinlich bekanntesten AI/ML NLP Bibliothek „word2vec“ von google gleichgesetzt. [4, 5]. Jedem Wort wird hierzu ein token, eine Zahl, zugeordnet und dieses token wird in einen hochdimensionalen Raum, typischer Weise mit 300 Dimensionen! eingebettet [6, 7, 8]. Die hohe Dimension des (Wort-) Raumes erlaubt es, Worte nach 300 Dimensionen zu differenzieren. Das Verblüffende ist, dass Neuronale Netzwerke, die mittels Texten trainiert werden, die Worte eines Textes nicht beliebig in diesem Raum verteilen, sondern gemäß Sinn, wie wir ihn auch wahrnehmen. Man kann dann sogar mit diesen Wortvektoren „rechnen“, z.B. König-Mann+Frau = Königin. Dieses Rechen hat auch dazu geführt, dass man Vorurteile und Diskriminierungen in Datensätzen aufgedeckt hat, also z.B. Arzt-Mann+Frau = Krankenschwester. – Wohlgemerkt, Datensätze die unsere diskriminierende Realität beschreiben.
Wer sich von der hinterlegten Technik beeindrucken lassen möchte, den verweise ich auf die word embedding Illustration von tensorflow [9].
Dies word embedding ist für mich eine mehr als nur erstaunliche Erfahrung. – Sie stützt einen meiner wichtigsten Glaubenssätze: „Das Sein unterscheidet nicht zwischen belebt und unbelebt, oder zwischen bewusst und unbewusst, wir treffen überall auf die gleichen fundamentalen Prinzipien, auch wenn deren Erscheinungen auf den ersten Blick sehr unterschiedlich sein mögen.“
Eine der bekanntesten NLP Bibilotheken, die word2vec Funktionalität integriert, ist spaCy [10]. Ich benutze spaCy, um SO(x, t) an einem einfachen Beispiel zu berechnen. Ich lehne mich an Beispiele aus [11] an und zeige im Folgenden den Code wie er in einem Jupyter Notebook [12] in der google Colab-Umgebung [13] lauffähig ist. Zunächst eine kleine Illustration von word embedding:
pip install spacy
!python -m spacy download en_core_web_md
import en_core_web_md
nlp = en_core_web_md.load()
vocab =nlp(‚cat dog tiger elephant bird monkey lion cheetah burger pizza food cheese wine salad noodles macaroni fruit vegetable‘)
words = [word.text for word in vocab]
vecs = np.vstack([word.vector for word in vocab if word.has_vector])
pca = PCA(n_components=2)
vecs_transformed = pca.fit_transform(vecs)
plt.figure(figsize=(20,15))
plt.scatter(vecs_transformed[:,0], vecs_transformed[:,1])
for word, coord in zip(words, vecs_transformed):
x,y = coord
plt.text(x,y, word, size=15)
plt.show()
Unter Anwendung des obigen Codes wird folgendes Bild erzeugt:

Ich gehe nicht auf die Details des Code-Beispiels ein, lediglich einige Hinweise, um das Wesentliche des Blogbeitrags zu erfassen: Ich benutze ein vortrainiertes englisches Vektormodell „en_core_web_md“ und übergebe diesem einige englische Worte ‚cat dog tiger elephant bird monkey lion cheetah burger pizza food cheese wine salad noodles macaroni fruit vegetable‘, die das vortrainierte Modell in einem 300-dimensionalen Vektorraum verortet. Um diese Verortung darstellen zu können, wird die Verortung mit der mathematischen Technik PCA auf zwei Dimensionen in der Abbildung 1 projiziert. – Dadurch kommt es zu visuellen Überlappungen, wie man im Bild sehen kann. Auch erkennt man sehr schön, dass das vortrainierte Modell gemäß der Bedeutung der Worte Bedeutungscluster gebildet hat.
Wenden wir uns jetzt der Similarity zu, indem wir die Similarity von Vektoren berechnen:

Abbildung 2 erläutert die beiden gebräuchlichen NLP Similarities. Word2vec verwendet hierbei lediglich die Cosine-Similarity. Werden ganze Sätze oder Texte auf Similarity geprüft „misst“ word2vec die Ähnlichkeit der Texte über Mittelwertbildung der beteiligten Vektoren bzw. Worte.
Die damit verbundenen Ergebnisse sind verblüffend, wie das nachfolgende einfache Beispiel zeigt:
doc1 = nlp(‚I visited England.‘)
doc2 = nlp(‚I went to London‘)
doc1.similarity(doc2)
Die Cosine-Similarity liegt für dieses Beispiel bei sα = 0,84. Die Similarity wird von word2vec auf den Bereich 0 bis 1 normiert (Anm.: Die Similarity könnte auch zwischen -1 und 1 liegen, was für unsere Betrachtung besser geeignet wäre).
Jedoch… die Euclidean-Similarity, berechnet mittels des Codes aus [14], ergibt eine sehr geringe Similarity von sr = 0,08.
D.h. Die Wordvektoren zeigen zwar in die gleiche Richtung liegen aber in völlig unterschiedlichen Raumbereichen des 300-dimensionalen Wortvektorraumes. – Beide Aussagen sind also nicht identisch, haben jedoch eine hohe Bedeutungs-Affinität.
Ein anderes Beispiel: Ich möchte die Similarity von zwei Texten aus unserem Buch Management 4.0 [15] vergleichen: Ich vergleiche eine Kurzfassung der Management 4.0 Definition mit der Langfassung der Definition:
doc1 = nlp(‚With a systemic leadership approach, Management 4.0 provides the guiding competence for viable learning organizations in complex situations and environments. Management 4.0 integrates an Agile Mindset, the universal principle of self-organization as a governance guideline, and relevant work techniques, for sustainable working models of the future.‘)
doc2 = nlp(‚We understand Agile Management as a leadership and management practice, to be able to act in an agile and proactive way in a complex environment characterized by uncertainty. It is described as an Agile Mindset with a focus on: leadership for which self-leadership is the basis; leadership, which is based on a respect for basic human needs; leadership, which demands an understanding of complex systems and promotes their regulation through iterative procedures; people who self-organize in teams; fluid organizations, which promote adaptable and fast delivery of useful results and create innovative customer solutions through proactive dealing with changes‘)
Das Ergebnis für die Cosine-Similarity, von word2vec, ist wieder verblüffend:
doc1.similarity(doc2)
sα = 0,97
Die Euclidean-Similarity berechnet mit dem Code aus [14] ergibt sr = 0,46. Also verglichen mit der Similarity aus dem vorherigen Beispiel sehr hoch.
Auf der Basis dieser Beispiel-Daten kann ich einen Beispiel Similarity-Operator angeben: Wir nehmen der Einfachheit wegen an, dass die obigen beiden Texte aus dem Management 4.0 Buch von zwei Personen gesprochen wurden. Damit ergibt sich der Collective Mind Operator dieser beiden Personen zu:
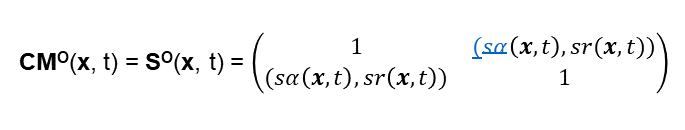
SO(x, t) ist eine symmetrische 2*2 Matrix (ich bitte darum, kleine farbliche Unsauberkeiten in der Formeldarstellung zu übersehen, hier bei sα): Die Nicht-Diagonal Elemente sind hier keine einfachen Skalare, sondern bilden jeweils einen Vektor in einem Similarity Raum. Da wir mit überschaubarer Mathematik (d.h. einfacher Matrizenrechnung) weiterkommen wollen, wandeln wir diese Vektoren in Skalare um. Die einfachste Weise, dies zu tun, ist sr(x,t) nicht zu berücksichtigen und die resultierende Größe als Skalar anzusehen. Ich könnte auch die Länge des Similarity-Vektors in die obige Matrix einsetzen. – Der Vektorbetrag wäre dann so etwas wie eine integrierte Similarity. – Das Weglassen von sr(x,t) hat im Rahmen dieser Vereinfachungen keinen wesentlichen Einfluss auf die nachfolgenden Ausführungen.
Damit ergibt sich:
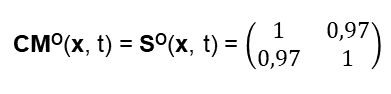
Man kann diese Matrix auch als sogenannte Heat Matrix darstellen, in dem die Similarities farblich codiert werden: Dies wurde in [16] benutzt, um die Similarity der Reden deutscher Politiker visuell darzustellen.
Wir haben bisher zwar einen Operator für den CM definiert, jedoch den CM selbst nicht ermittelt. Dies tue ich jetzt:
Für den Operator CMO(x, t) können wir sogenannte Eigenwerte und Eigenvektoren berechnen. Eigenvektoren sind diejenigen Vektoren, die unter der Anwendung des Operators lediglich ihren Betrag verändern, jedoch ihre Richtung beibehalten. Die Veränderung des Betrages bei Anwendung des Operators wird Eigenwert genannt. Den größten Eigenwert und dessen zugehörigen Eigenvektor assoziiere ich mit dem Collective Mind Vektor CMvektor dieser beiden kommunizierenden Personen (es gibt noch einen zweiten Eigenwert und Eigenvektor, der aber hier (wahrscheinlich) keinen Sinn machen):
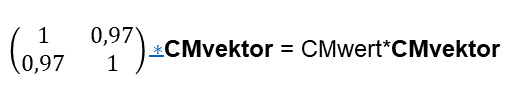
Das Internet stellt auch für solche Berechnungen eine App zur Verfügung [17]. Der Vektor CM bekommt damit folgende mathematische Gestalt:
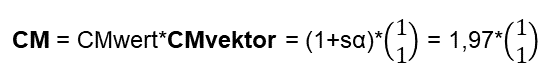
Der Eigenvektor liegt also auf der „Diagonalen zwischen zwei Personen“ und hat einen Eigenwert der größer als 1 und maximal 2 ist. Die Mathematik spiegelt mein Verständnis eines CM wider. Deshalb sage ich: „Gar nicht schlecht für den Anfang 😉, jedoch werden Synergieeffekte (d.h. Eigenwerte größer 2) und Effekte des gegenseitigen Blockierens (d.h. Eigenwerte kleiner 1) nicht abgebildet. Letzteres hängt auch damit zusammen, dass die word2vec Similarity per Definition nicht kleiner Null ist.
In unserem Beispiel ist der Eigenvektor und der Eigenwert statisch, da die Similarity keine explizite Zeitabhängigkeit enthält. Im Allgemeinen ist die Similarity eine zeit- und ortsabhängige Größe. Damit werden die Berechnungen viel aufwendiger, unterscheiden sich jedoch nicht von den einfachen Ausführungen hier.
Es ist also möglich Zeitscheiben zu definieren, in denen eine AI synchron in Teammeetings die Gespräche aufnimmt, die Gespräche transkribiert und dann wie hier geschildert (und evtl. mit weiteren AI Techniken) die Similarity berechnet. Die Darstellung der Similarity als Zeitreihen und des zeitlichen Verlaufes des Vektors CM könnte als Feedback-Mechansimus eingesetzt werden, um eine Teamreflexion zu unterstützen. – Die AI übernimmt damit eine „Coaching“ Funktion. – Dieser Blog-Beitrag skizziert also die Ausgestaltung der AI-Anwendung Collective Mind im IPMA Kompetenz Bereich Teamarbeit, aus meinem Dezember 2021 Blog-Beitrag.
[1] Köhler J, Oswald A. (2009) Die Collective Mind Methode, Projekterfolg durch Soft Skills, Springer Verlag
[2] Armatowski S., Herrmann P., Müller M., Schaffitzel N., Wagner R (2021) The importance of Mindset, Culture and Atmosphere for Self-Organisation in Projects, White Paper IPMA, erstellt anläßlich der IPMA Research Conference 2020
[3] tensorflow (2022) tensorflow.org, zugegriffen am 16.04.2022
[4] google (2022) word2vec, https://code.google.com/archive/p/word2vec/, zugegriffen am 16.04.2022
[5] Wikipedia (2022) word2vec, https://en.wikipedia.org/wiki/Word2vec, zugegriffen am 16.04.2022
[6] Karani D (2022) Introduction to Word Embedding and Word2Vec, https://towardsdatascience.com/introduction-to-word-embedding-and-word2vec-652d0c2060fa, zugegriffen am 20.04.2022
[7] Megret P (2021) Gensim word2vec tutorial, https://www.kaggle.com/pierremegret/gensim-word2vec-tutorial , zugegriffen am 20.04.2022
[8] Delaney J (2021) Visualizing Word Vectors with t-SNE, https://www.kaggle.com/jeffd23/visualizing-word-vectors-with-t-sne/notebook , zugegriffen am 20.04.2022
[9] word embedding playground (2022) http://projector.tensorflow.org/
[10] Spacy (2022) https://spacy.io/models/de, zugegriffen am 20.04.2022
[11] Altinok D (2021) Mastering spaCy, Verlag Packt, kindle edition
[12] Jupyter Notebooks (2021) https://jupyter.org/, zugegriffen am 02.12.2021
[13] Colab (2021) https://colab.research.google.com/
[14] NewsCatcher Engineering Team (2022) https://newscatcherapi.com/blog/ultimate-guide-to-text-similarity-with-python, zugegriffen am 20.04.2022
[15] Oswald A, Müller W (2019) Management 4.0 – Handbook for Agile Practices, Verlag BoD, kindle edition
[16] Timmermann T (2022) https://blog.codecentric.de/2019/03/natural-language-processing-basics/, zugegriffen am 20.04.2022
[17] Виктор Мухачев (2022) https://matrixcalc.org/de/, zugegriffen am 20.04.2022